What Is Intuition? Cognition, Thinking, and Emotion (Column 653)

With God’s help

Disclaimer: This post was translated from Hebrew using AI (ChatGPT 5 Thinking), so there may be inaccuracies or nuances lost. If something seems unclear, please refer to the Hebrew original or contact us for clarification.

In the previous column I needed a general characterization of the faculty we call intuition. I searched the site and was surprised to find that although I’ve discussed it in many places, there isn’t a single orderly column that does so systematically. So I decided to fill that gap here.

Intuition Is Not Emotion

First, I wish to dismiss the common association between intuition and emotion. Emotions are not claims. When I say that I love someone and someone else says that he does not love that person, we are not in disagreement. There’s no disputing taste and smell. Note: that is not because the dispute cannot be resolved but because there is nothing to resolve (there is no dispute here). These are two reports about mental states—mine and his—not a claim about something in the world. The fact that I am in mental state A does not contradict the assertion that so-and-so is in mental state B. Each person has his own psychological makeup. Even if we look at just one assertion, say mine, it cannot be judged in terms of truth or falsehood. I am not asserting anything about the world but reporting a state within me. Hence I do not disagree with someone who feels differently. Likewise, when I say that I am afraid and someone else says that he is not—there is no disagreement. Again, these are reports about inner psychological states in different people. Of course, if someone claims that I am not afraid (that is, his claim is about me and not about himself), then we do have a dispute—but that is not my topic here.

Now consider Reuven, who has invested great effort over years in solving a very difficult scientific or mathematical problem. At long last he reaches an answer, X, and holds a thanksgiving party for friends in that scientific community. At the party Reuven presents the problem to his colleagues, and suddenly one of them, Shimon, stops him and says: “Oh, obviously, the solution is X.” Reuven is stunned, for he labored over this problem for years with his best talents and energy, and Shimon tosses out the answer offhand a moment after hearing the problem. Reuven, with trepidation, asks Shimon how he managed to solve it so quickly, and he replies: “When I saw the problem, I had a strong feeling that this is the solution.”

Is the term “feeling/emotion” appropriate here? I don’t think so. We saw above that an emotion denotes a report about a mental state, and therefore there is no point arguing about it. Is what Shimon proposed an emotion in that sense? His solution is a claim about the problem before us, and as such it can be true or false. Now think about someone else, say Levi, who says “the solution is Y” (because he has such a feeling, and not Emotion X like Shimon). Clearly Levi disagrees with Reuven and Shimon (who hold that the solution is X). That is, the assertion that the solution to the problem is X or Y is a claim, and anyone who disagrees is in a dispute with us. In that sense, we are not dealing with an emotion here.

Why, then, are we inclined to treat this as an emotion? Because the answer here is not argued for. Reuven’s assertion is not considered an emotion but the result of reasoning. Shimon, however, reached the same result without calculation but only on the basis of a “feeling,” and therefore in his case it seems to us like an emotion rather than reasoning. The same goes for Levi, who reached a different result. Yet the term “emotion” in this context is not apt. They are not presenting a calculation, but if we examine their solutions we can determine which of them was right and which was wrong. In other words, this is a claim and not a report about a mental state. In affective psychological states, emotion is merely a report about that state and nothing more. But in solutions to scientific or mathematical problems, the mental state produced an insight, and that insight is a claim subject to truth or falsehood.

Thus, none of our three friends is dealing with emotions. They are all making claims. The difference between Reuven and Shimon on the one hand and Levi on the other is a disagreement about a claim—indeed a factual dispute (whether X is correct or Y). The difference between Reuven and Shimon is not a disagreement at all, since both assert the same claim (X). Here the difference is only in the way they arrive at the claim. Reuven reached it through recursive, conscious, rational thinking, while Shimon reached it by intuition. Intuition is not an emotion but a cognitive–intellectual faculty. As noted, using the term “emotion” in such a context is very confusing. It is better to distinguish between them and call affective states “emotions,” whereas direct cognitions (not based on step-by-step reasoning) I propose to call “intuitions.” In this view, we can say that Reuven and Shimon are running Achilles and the Tortoise’s race. Reuven is the tortoise, who solves the problem step by step in a systematic way with explicit and detailed calculation. Shimon, by contrast, is Achilles, who covers the distance quickly and gets straight to the final result without passing through all the intermediate steps. It is entirely possible that in Shimon’s brain all of Reuven’s steps were performed, but rapidly and without awareness (below I will mention Daniel Kahneman’s System 1 in this context).

Another example can be found on my site, in column 471, where I discussed the Talmud’s permission for Zimri to kill Pinhas under the rubric of “pursuer” (rodef). That is highly counterintuitive, since Zimri was the offender and Pinhas sought to prevent the offense and even received God’s blessing for what he did. And yet, the Talmud says that from Zimri’s perspective Pinhas is a pursuer and he is entitled to kill him in self-defense. In a comment there Avi cited a distinction by the Rosh on the spot, who writes that this permission was given only to Zimri himself and to no one else:

But another person would be executed for killing him, for he [Pinhas] is not a full-fledged pursuer since he acts with authorization. And specifically Zimri is permitted to save himself at the cost of Pinhas’s life, but not any other person. For every other person is given license to kill Zimri; therefore he [Zimri] has no license to save himself by taking Pinhas’s life.

The rationale for the Rosh’s distinction is not so simple (see my brief response there), but my intuition clearly says that the distinction is correct. After that one can try to formulate a systematic, orderly rationale, but the intuition gave us the answer immediately. The fact that we later found a rationale only shows that this intuition is not merely a subjective emotion detached from truth and reasoning. It is an unconscious reasoning that arrives at a “correct” conclusion—that is, at a claim and not an emotion—even though it skips the recursive procedures of our ordinary thinking.

The Relationship Between Emotions and Facts

The conclusion is that our intuition is a rational or cognitive faculty, not merely a given psychological structure. There is no reason to take seriously conclusions that arise from my psychological makeup. As Mark Twain said, “The world owes you nothing; it was here first.” The fact that you are built a certain way says nothing about the world, and therefore whatever follows from your mental makeup cannot be a factual claim about the world. A psychological structure produces emotions (like love or fear), but intuition is part of our intellect that apprehends the world.

True, when I love Rachel, this is of course related to various of her characteristics that arouse in me the emotion of love. But someone else will feel love toward Leah and not toward Rachel, because his psychological makeup is stirred by different features than those that stir me. So yes, there is a connection between emotions and facts, but the existence of the emotion as such yields no factual claim and says nothing about the world.

The example of fear is subtler and more complex. Fear can arise from facts. For example, when I encounter a predator, fear arises in me. That fear results from the information that such an encounter may end badly for me. But this is not a conclusion from the existence of the emotion of fear itself, but from the information that arouses the fear. If I conclude that the emotion of fear expresses a factual insight (acquired from experience or some other source), namely that a predator is something one should beware of, then fear can be seen as a source for factual claims. But again, the existence of fear as such does not say that. What matters is the information that the fear reflects. Consider a person with a damaged brain who does not feel fear; he can still understand that a lion is dangerous and draw the conclusions and run away. In him, that information does not manifest as fear, but what matters on the factual level is the information, not its affective form. As noted, what goes on inside me due to my mental makeup cannot serve as a basis for a factual claim about the world.

In other words, when I encounter a lion I have an intuition that there is a serious danger to my well-being. My psychological makeup is such that the information conveyed by the intuition generates within me the mental state of fear, and then I flee. But the fear is only a mediator and not the source of that information. Just as a sensation of pain says nothing on its own. In a normal person, if he feels pain there is probably a physiological source, and therefore he would be wise to check and treat it. But the pain is only an indicator that mediates the physiological damage to my psyche. I do not go to be examined because of the pain but because of the information the pain expresses. Even a person who lacks pain sensation, upon discovering the same medical problem, ought to go to a doctor.

For my part, even when I respond to information conveyed to me through the mediation of emotions, I am not responding to the emotions and I am not basing myself on them. It is based on the assumption that an emotion of this kind reflects some factual state, and that state—not the emotion—is my motive for action and decision. I once wrote that the feeling of love for a woman is not a reason to marry her. It is one datum to be weighed when forming a decision whether to marry or not. That decision should be made with the intellect, not with emotion.

What Is Intuition: Characteristics and Sources

In Wikipedia, s.v. “Intuition,” we find the following definition:

Intuition is rapid inference based on a paucity of data by means of past experience and past inferences.

The ability to receive and decipher intra-personal messages (to attain knowledge) without deliberative thinking. What characterizes intuitive knowledge is the fact that it is generated very quickly (in an instant) and appears suddenly (as inspiration or a flash). Nevertheless, the intuitive solution is not always created immediately.

A person who holds an intuitive insight cannot fully explain why he adopts that position. In this, intuition differs from opinion; to the contrary, often intuitive knowledge contradicts a person’s ordinary logic and challenges him to decipher it. In this respect it also differs from instinct, which is an innate inner tendency based on prior experiences and whose purpose is survival.

There are two points here: the definition of intuition and its sources. Regarding its definition, intuition operates unconsciously and not on the basis of arguments and systematic reasoning. That is exactly what we saw above in Shimon’s solution of the problem.

The Israeli psychologist Daniel Kahneman, Nobel laureate in economics, explained in his book Thinking, Fast and Slow that there are two systems of thought within us: System 1 is fast, instinctive, and emotional, and System 2 is conscious, rational, and slower. In most of our functions, System 1 works better and more efficiently, though in complex problems—and in particular when we have cognitive biases in the matter at hand—we will need System 2. Some people have a more developed System 1 and can use it even to solve scientific and mathematical problems (like Shimon above). In the domain of morality, too, this system is widely used. In many cases our moral stance toward a given situation is not the result of reasoned thinking but of a feeling—what we call “conscience.” Here, too, my claim is that this is not an emotion but an intuition. If it were an emotion, that ethical judgment would have no validity (as we saw regarding emotions in general). We can link Kahneman’s System 1 to intuition and System 2 to conscious reasoning. Below I will argue that this linkage is not exact and not complete.

So much for the nature of intuition. But, as noted, this Wikipedia passage makes another claim about the source of intuition. It contends that this ability is the product of experience and past inferences (or prior experiences). Later in the entry we find the view of psychoanalyst and psychiatrist Carl Jung, who said something similar:

Intuition is an immediate approach to the experience of the inner unconscious of each person. According to him, an action driven by intuition or a gut feeling is essentially the opening of one’s mind to inner feelings and thoughts, balanced against the information apprehended by the senses.

I think this thesis represents the common conception that intuition is nothing but accumulated experience stored in our subconscious over the years, which manages to break out from time to time and guide us in decisions and interpretations of various situations. It can be likened to training a neural network (an artificial brain), into which data are fed, each item re-organizing the network so that it internalizes it. After a while, the network can solve new problems in light of its accumulated “experience.” This means that intuition is nothing but the product of a collection of cognitions that act upon our brain and shape it in accordance with what emerges from them. These cognitions sometimes reach our conscious thought, but they also enter our subconscious and accumulate there. They also emerge from there in an uncontrolled way; in fact the products of this experience burst forth when needed and help us solve new problems based on that accumulated, unconscious experience. This is Kahneman’s System 1, and according to this claim its source is experience.

Most people I have spoken with do not even consider the possibility of another way to understand intuition. For them it is clear that we are dealing with the accumulation of experience through our cognitive faculties. In their view, the only difference between it and ordinary reasoning is the absence of awareness. I now wish to argue that experience cannot be the sole source of intuition. There must be something more there.

Intuition Cannot Be Only Accumulated Experience

In column 426 I discussed Occam’s razor, which at least today serves as a generic name for preferring a simpler explanation over a less simple one. If there are two theories that both explain all the facts, we choose the simpler. But the fact that it is simpler does not mean it is the correct one—particularly since simplicity is debatable (what is simple to me may not be simple to you, and certainly not to a being structured entirely differently from humans). Hence many construe the principle as methodological–psychological, not as a tool for arriving at truth. If there are two theories that explain all the facts and one is simpler, why not use it? The choice is a methodological principle, not because it is more true.

In that column I presented an argument showing that the razor is a tool for uncovering truth, not just a methodological principle. The argument was based on the fact that any set of experimental results can fit countless generalizations. Thus, in the graph below we see results of several measurements regarding the relation between the force acting on a body and the acceleration it develops (Newton’s second law of mechanics):

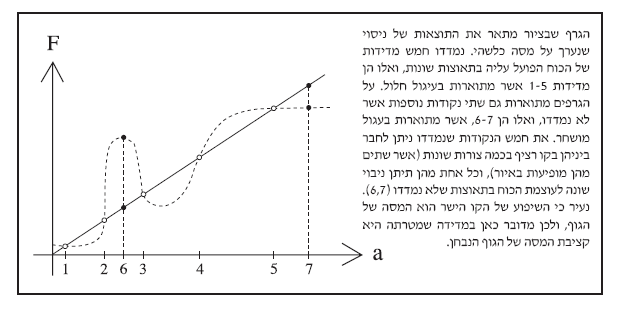
We obtain five results in experiments (the points marked with hollow circles). A scientist will try to draw a line through these results in order to obtain the general law (the law that holds for any force and any acceleration). Philosopher of science Carl Hempel called this process the “deductive–nomological schema.” He showed that explaining phenomena we measured by means of a theory is essentially the search for a general law of which the cases we measured are particular instances (derivable from it by deduction). In the case described there, the natural line is a straight line (the solid line drawn). But as you can see, there are many other ways to draw a line through the five measured points (one such is indicated by the dashed line), and therefore from those five measurements we can reach innumerable generalizations, that is, innumerable general laws. The straight line is indeed the simplest, but, as stated, that does not necessarily mean it is also the most correct. Similarly, in any formulation of a scientific theory from empirical findings, one can reach innumerable general theories of which the cases we measured would be particular instances.

According to this approach (which I called, following Zeev Bechler, “actualism”), the conclusion that the general law is a straight line (F = m·a), or that the simplest theory is the “correct” one, is construed as a tentative conclusion. As long as we have not found a contradiction to this being the correct line (or correct theory), we will use it because it is the simplest—but we are not asserting that it is indeed the correct one. Note: the actualist is not merely claiming that we cannot have certainty about this line. No one disputes that. A scientific theory always subjects its predictions to tests of refutation. The actualist’s claim is that there is no reason at all to suppose that this is the correct line—or, say, that it is more correct than the dashed line. In his view, we choose this line because it is simpler. This is our decision for reasons of convenience, not a claim about the world. That’s all. On this view, our intuitive feeling that the straight line is the correct line (or more generally that the simpler theory is also more correct) is but a product of the way our subjective intellect works and has nothing to do with what happens in the world itself. It is an expression of the notion that intuition is an emotion. In this sense, one can say that the theory is merely a report about a mental state (in the scientist’s mind) and not a claim about the world.

But as I showed there, this approach does not withstand the test of facts and logic. We saw that for the actualist the theory is merely a convenient way of arranging known facts, not a claim about the world. On this view, the probability that in the next experiment (say, when we measure point 6 or 7 in the graph) we will get the result that lies on the straight line is zero (for each line yields a different result, and the actualist assumes that as far as the world is concerned all lines are of equal status). Is that really what happens in our scientific experiments? When we test a scientific theory formed by generalizing measured cases, do its predictions always fail in the next experiment? That is what would follow if the actualist were right. For him every theory is a shot in the dark, an arbitrary choice among countless possibilities, having nothing to do with the factual truth about the world itself.

Yet if the actualist were truly right, we would today be at the scientific knowledge level of Adam. Every experiment would fail and force us to replace the theory. We would be swapping theory for theory after each experiment, chasing our own tails throughout the history of scientific research. There would be no progress in our understanding of the world. But that is not what actually happens. In fact, quite a few experiments do succeed (of course some fail, but not all; for our purposes that suffices). This means that our intuition—our ability to “guess” the correct line, or what we regard as the “simplest”—is not merely an emotion but some cognitive instrument. This instrument leads us to results that make claims about the world, and therefore they are not subjective emotions (which, as we saw, make no claim about the world). It enables us to advance in the scientific understanding of the world—that is, it is a device for arriving (in many cases) at correct theories about the world itself.

The conclusion so far is that intuition is not an emotion but a tool that reveals factual truth. Moreover, it is clear that intuition is not pure reasoning. If it were pure reasoning, then the path from the data we measured to the theory could not lead us to the correct conclusion. The data themselves can be generalized in many ways, and reasoning without observation cannot sort out the correct generalization. Reasoning can tell us which generalization is the simplest (in the scientist’s eyes), but the decision that the simple is also correct is a mere baseless conjecture (essentially a subjective emotion). Therefore it is clear that the basis of scientific generalizations must also include an element of cognition beyond reasoning. From viewing the five results we measured, we “see” that the straight line is the correct law.

I elaborated on this in my series on Intellectual Optimism and Pessimism (494 – 496). There I explained that the route to synthetic-a priori claims must contain a cognitive component and not only processes of reasoning. Kant’s problem of the synthetic a priori arises only because of the tacit assumption of a sharp distinction between reasoning and cognition (and therefore Kant, who would not relinquish that assumption, could not solve it), and its solution necessarily involves relinquishing that dichotomy. Kant’s problem compels us to conclude that we have thinking cognition or cognizing thought (see also the previous column). The route from measurements to general laws (the generalization) is not a purely intellectual process. It includes an observational–cognitive element, even if not mediated by the senses. We have a sixth sense—namely, a department of the intellect that engages in intellectual “seeing” of the world (what Husserl called “eidetic vision,” Maimonides “the eyes of the intellect,” and Rav Ha-Nazir “auditory logic.” All these expressions combine an element of reasoning with an element of cognition and mean that our intellect has a function that integrates both). Husserl describes it as though the specific data are “transparent,” and we “see” through them (with the eyes of the intellect, eidetic vision) the general law.

Thus, intuition is neither emotion nor (mere) reasoning but a cognitive instrument. We can still ask whether this instrument is only the product of accumulated experience, or whether there is something beyond that. If you think a moment longer you will realize that from the same argument I presented here (from the graph) we can also see that it is not merely accumulated experience. To understand this we must note that accumulated experience itself is nothing but a generalization based on specific cases we observed. We must understand that learning from experience always involves generalization. The next case I encounter will never be the very case I already observed. Even if it were the same situation, I would still need the assumption that it will behave the same way as before (that is, the assumption that there is a fixed law is our assumption, not something arising from observations). But as we saw, any set of cases can be construed—that is, generalized to a general law—in innumerable different ways. How, then, can one learn from experience at all? How can one choose the correct generalization on the basis of the facts observed?

The inevitable conclusion is that intuition cannot be only a process of reasoning. It contains a cognitive dimension. Intuition is also based on direct cognition. My way of realizing that the straight line is the correct general law is neither a subjective emotion nor merely the result of accumulated experience. The “simplicity” of the straight line expresses that I “see” (with the eyes of the intellect) that it is the more correct line. We have the ability to look at the measurements we made, to see “through” them the general law, and to understand that it is precisely the straight line and not any other line that strings all these observations together (like the dashed line in the drawing). This is the only way to explain how the choices we make (what seems to us the simplest way) are not arbitrary and in many cases their predictions match the future observations we will make.

Interim Summary: Four Different Conceptions of Intuition

We rejected the possibility that intuition is emotion. We then saw that it also cannot be pure reasoning (that is, intellectual processing of specific data), but must include an observational component. Yet even that is not the end of the road. We saw that intuition is not only the product of prior observations (accumulated experience), but contains a component of direct observation (with the “eyes of the intellect”). As if contemplation of the data transfers us directly to the general law that explains them (they are its particular instances).

Applications to Artificial Intelligence

Here a difficult question arises. If this is indeed based on an innate faculty (a kind of intellectual perception) and not only on accumulated experience, we would expect that an artificial intelligence system would not be able to learn from experience. But in fact such systems do learn from experience just as we do (and sometimes better). I noted above that the common way of “training” a neural network is to feed it data, which it internalizes and shapes itself accordingly, and after sufficient experience it can solve new problems based on that experience.

Do computers also possess the faculty of eidetic perception? That already sounds thoroughly mystical. Computers perform mechanical calculations, and if learning from experience—which is a collection of generalizations from the data we encountered—cannot be merely a process of reasoning, i.e., if it must contain an element of direct cognition of the general law through the data, that should not occur in a mechanical artificial system. It merely processes the data and produces a generalization from them. If an artificial system succeeds in learning from experience, it would seem to be evidence that we are dealing with data processing, i.e., a process of pure reasoning without an additional observational component (beyond collecting the data themselves).

We can sharpen the analogy to artificial reasoning through the fact that the way an AI system makes decisions is very similar to what I described above regarding the graph. We are dealing with a collection of methods called regression, used to derive a relation between an independent variable and a dependent variable from specific data in hand (from measurement or another source). In a typical first lesson in a machine-learning course, students learn the (non-statistical) regression technique familiar to every scientist as the “least squares” method.

Here is an image from Wikipedia depicting measurements of the relation between age and height in children:

How do we draw the solid line that strings these points together? You can see that the situation is less clear than in the graph I brought above; it’s not certain that we’re dealing with a straight line, though that looks plausible. But even assuming the line is straight, its slope is not obvious (there is some wiggle room). In addition, if you want to guess how this continues at later ages, it would be very risky to use this graph for prediction. It depicts the growth period, but at some stage the child stops growing and the graph levels off (asymptotically to final height, and perhaps even declines at more advanced ages). Moreover, even in the growth period there is no reason to assume that the growth rate is constant (i.e., that the graph is linear).

What we do in such a case is assume, based on the overall impression, that it is a straight line—at least up to the relevant age—and then look for the line that best fits the results (i.e., the values of the two parameters of that straight line). The common criterion for “best fit” is “least squares,” that is, we seek the line that minimizes the sum of distances of the points from it, and assume that this is the correct line. Of course, it may be that the correct line is not straight at all. It may be some wildly different curve that strings the points in a completely different way (like the dashed line in the earlier graph). But the researcher assumes some form of line (according to a visual impression of the results), and then tells the AI software to find the straight line that best fits these results—just as a scientist does in the Newton’s second law example.

That is, the AI software assumes in advance the shape of the correct line, and only then can it search for the exact line that best fits the results. Even the criterion by which we determine the fit is not univocal. “Least squares” is only one of several options. If we assume a different type of line (not straight), still, once we assume some fitting criterion we can find the best-fitting line. If there are several possibilities we choose the simplest line (with the straight line, in our eyes, being the simplest, of course).

We can extend this to more complex datasets, where the shape of the correct curve is not at all clear, and there the researcher must decide on some curve shape and only then seek a fit (the parameters of the best-fitting curve). There are also points that deviate significantly from the general trend, which we may assume are errors and discard (not take into account). But all these are intuitive decisions by the researcher, and they are given as inputs to the AI software. I note that nowadays there are programs that can suggest the curve shape on their own, but they too are fed with principles dictated by the human programmer/researcher.

In column 592 I discussed cognizing thought as a human faculty and wondered whether it exists in AI or not. As I understand it, it exists in the programmer, not in the software, and therefore it is a mistake to view the software as a substitute for human thought. A person built a tool based on his insights, and it is no wonder that the tool succeeds in human tasks. That does not mean that a being who is a blank slate relying only on experience would succeed. The computer is not a blank slate and it does not rely only on experience (i.e., only on the cases it is “trained” on). It is imbued with insights whose source is in us, just as they are imbued in us.

Intuition from the Scientific–Empirical Angle

The conclusion is that there is no such thing as pure learning from experience without presuppositions and a conceptual framework. Even what appears to us as unadulterated experience—what the typical empiricist would happily rely on—contains within it a priori principles drawn from our intuition, whether or not we are aware of them. So too with the empirical character of modern science. I have often pointed out that many people live under the illusion that science is based only on observations and does not assume anything beyond what is based on direct observation. That is a misunderstanding. At the base of science lie innumerable assumptions that have no empirical source (the principle of causality, induction, the rejection of action at a distance, and much more). That is, both the human learner and the “learning” AI are not nourished only by specific facts. They do not come to research as a blank slate, but laden with assumptions and modes of thought—without which it is impossible to learn and progress. That is also what we saw in the graph example above.

This of course raises the question: what justifies the trust we place in these assumptions? Note, the question is not whether we hold them to be certain. We do not. The question is: why take them seriously at all? Are they not merely assumptions grounded in the structure of our thinking, to which the world owes nothing? The possibility of trusting them derives from the assumption that we have some faculty capable of generating and granting us such insights, not from sensory observations. This faculty precedes observation and undergirds our ability to use it. But it is not an emotion and not merely a subjective matter, since the information based on it counts for us as reliable information, and we rely on it without hesitation. Thus, at least from our perspective it is clear that this is a cognitive faculty capable of saying things about the world even prior to observation, and indeed grounding our ability to learn from observations.

Intuition from the Philosophical Angle

At the base of our thinking and our accumulation of knowledge about the world lie two fundamental toolboxes: the scientific–empirical and the logical–philosophical. The former is grounded in observation; the latter, in reasoning. So far we have seen that at the base of our ability to learn from experience and observations lies an a priori faculty that I called intuition. We saw that it outlines the framework within which we learn from experience and interpret observational facts—i.e., it undergirds science.

But intuition also lies at the base of the second toolbox, the logical–philosophical. Every logical and philosophical argument is grounded in first principles. These premises themselves can perhaps be derived from still more fundamental premises, but at the end of the road there is a set of basic premises not derived from prior ones. These are our axioms or self-evident truths. Where do we get them? Experience cannot furnish us with all our first principles, for several reasons: first, we saw that experience itself is grounded in a priori assumptions. Second, experience yields particular facts (a particular object fell to earth; a particular person told me the correct time of day, etc.). From that one cannot logically derive any general insight about the world—and certainly not the laws of nature. To move from isolated observations to the laws of nature requires generalization, which is grounded in reasoning and a priori assumptions (and above we saw that these themselves cannot be merely the product of accumulated experience). Thus, at the base of the premises of our logical arguments lies intuition. Upon it rests our entire philosophical edifice, for if we have no trust in the first principles, what value is there in the structure we build upon them?! Intuition is a cognitive component that imports into us information about the world and about how to handle and reason about it. In my series on philosophy (155 – 160) I showed that the whole field called “philosophy” is nothing but the systematic collection of these insights/cognitions and an analysis of their import.

In addition, we saw above that sometimes intuition shortens the path of recursive reasoning (this is likely what happens in the example of Reuven and Shimon’s problem above). In such cases one could say that it contains no cognitive component but merely performs the computation/reasoning unconsciously. In principle it is possible to perform that computation consciously and slowly, step by step (like Reuven), but a gifted person (like Shimon) can do it quickly without awareness. It is the very same computation that Reuven performs but carried out inside Shimon.

Back to Kahneman

Kahneman’s System 1 deals with processes of reasoning that do not involve explicitly formulating the argument and the calculation, but arrive directly at the conclusion (as in the example of Reuven and Shimon). This itself can be construed in two ways: (1) Shimon looks at the equation or the problem and “sees” with the eyes of the intellect the solution. Here there is an element of (unconscious) cognition. If that is the process, there is no possibility of formulating a conscious, slow equivalent. (2) Shimon performs all the computational steps but unconsciously. In this account there is no cognitive component, yet in principle one can formulate a conscious, slow equivalent: simply describe the calculation step by step (this is exactly what Reuven did, and the assumption is that Shimon and he traversed the very same route—Shimon quickly and without awareness, Reuven consciously and slowly). In Kahneman’s terms we can say that Shimon has a highly developed System 1, whereas here Reuven uses his System 2.

When intuition yields our first principles or the methodological framework within which science operates, there it is clear we are not dealing with a shortcut of reasoning. Arriving at first principles or at the framework of scientific thought are processes that have no conscious counterpart (recursive or not). This is intuition as a process of cognition, not a shortcut of reasoning. Therefore I wrote above that identifying Kahneman’s System 1 with intuition is not precise. In his System 1, Kahneman treats intuition as unconscious computation—yet in principle it has a conscious counterpart. If we proceed slowly and consciously, like the tortoise, we can formulate the calculation and perform it step by step and reach Shimon’s result (as Reuven did). But the route to first principles is not unconscious reasoning; it is a non-sensory perception of the world. As I explained, there cannot be a conscious or sensory counterpart to that. One who lacks it will never get there. Here only Achilles (Shimon) will manage to solve the problem; the tortoise (Reuven) lacks the tools to do so.

Intuition and Faith

This brings me to the relation between faith and intuition. We saw that the base of our first principles and our conceptual framework is built by intuition. This is a non-sensory perception of the world that yields claims about it (without using the senses or philosophical proofs). If so, science (sensory observations and learning from them) and philosophy are built upon intuition, not vice versa. Therefore the doubt “what is the validity of intuition?” reflects a misunderstanding. It expects an explanation that would grant intuition validity by force of a logical argument or on the basis of an observation or scientific finding. But the logical order is the reverse: they are built on intuition, not it on them—“Your guarantor needs a guarantor.” On the face of it, relying on it seems like an irrational and illogical tool. But once you understand what I have described here, you see that the picture is exactly the opposite. This is the foundation of all rational and scientific thinking. They rely on it, not it on them. It is the most basic foundation of rationality, and therefore its own rationality is not in doubt.

In this sense one can say that “intuition” is a synonym for “faith.” Faith is a claim we accept without having an observational basis for it. And even if we have a logical–philosophical argument, that argument itself is grounded in first principles that themselves lack such a basis. Hence people commonly say that faith is an irrational claim, perhaps an emotion. The punctilious add that where philosophy ends, faith begins. We are dealing with insights we reach without observation and without foundation. But in light of what I have described so far, the truth seems the reverse. Faith is not an emotion; otherwise the believer would not differ from the atheist except in psychological makeup. They would have no substantive dispute. Yet faith is also not based on observation or philosophy; rather, it is their foundation. Seemingly it is unfounded and irrational—but in truth it is the essence of rationality, which is entirely grounded in intuition, i.e., in faith. A principled rejection of intuition is a renunciation of rationality altogether (and of science as well).

On this view, at the foundation of all scientific or other knowledge lie beliefs, that is, insights grounded in intuition. Faith is the foundation of rationality and logic, not a substitute for them. I am speaking here of faith as a faculty (that is, the tool I have called “intuition”), not of particular beliefs—whether in God or anything else. I have confidence in this tool and in the insights I derive by means of it—about the world, about morality, or any other field. Belief in God is just a special case of these beliefs. It is a product of our intuitions, and the logical arguments that lead to it only expose that it resides in the first principles on which those arguments are built (see my essay here).

This brings me to a question Yonatan raised in the Q&A a few days ago:

What do you think of the following statement (by Rav Kook):

“Faith is neither intellect nor emotion, but the most fundamental self-disclosure of the essence of the soul, which must guide it in its disposition.”

To which I replied with my characteristic delicacy:

If only I understood what that means. I suspect that no one else (including the speaker) truly understands it either. In the next column I will sharpen a point that may relate to this saying.

So here is the column, and here is my response to the shock Yonatan expressed there at my apparent disparagement of Rav Kook. I am not disparaging him, but to my judgment his writings are full of vague statements with undefined concepts, and therefore also full of claims that sound profound only because we have not bothered to define the terms. Once we define them, we sometimes discover that we are dealing with imprecise statements—if they have any meaning at all. I have written more than once that there is nothing outside our thinking and intellect. These are the tools we have, and whatever lies beyond them is nonsense—or at least asserts nothing. Therefore faith, too, cannot be beyond the intellect (and, as noted, it is certainly not an emotion). That is why I wrote there that when such a thing is said, one must first define what “intellect” is and what “emotion” is, and then one can say something about the relation of these two to faith. As we have seen here, faith is the product of the faculty called intuition, and that faculty undergirds all rational and scientific thought, and therefore it cannot be something different from them.

For me, where intuition (faith) ends, philosophy and science begin—not the other way around. Whoever wishes to claim otherwise should kindly explain where our intuitive insights come from, which are neither emotion nor observation (not even accumulated past observations embedded unconsciously). Is there some faculty other than what is called faith? How do they differ? Why assume at all that they differ? They sound and look the same, so what is the basis for and benefit of the claim that we are dealing with two different faculties? My sense is that the motivation for such outlandish statements is the desire to aggrandize faith. But as Maimonides writes about those who think that giving no reason for the commandments magnifies God, it is exactly the reverse: to say that faith is above the intellect is to say that we are dealing with nonsense. That is, such a person testifies about himself that he does not truly believe in God and His existence, but has certain experiences. If it is not intellect then it is emotion, for there is no third option. Emotions—or what is “above the intellect”—have nothing to do with faith.

I do not intend to claim that Rav Kook or others who say such things are not believers. Clearly he was a great believer. My claim is that they sometimes use undefined and confused concepts. In fact they believe in God because their intellect (and their intuition) tells them that God exists, but they do not understand this (because we are dealing with unargued statements, and relying on them calls for justification), and therefore they describe it as something that is emotion or that is above the intellect, and the like. As noted, these are unnecessary and incorrect statements, and they do not magnify God or faith in Him in any way. The opposite is true.