The Halakhic Meaning of Multiplying Probabilities: B. Safek Sefeka (Double Doubt) (Column 613)

With God’s help

Disclaimer: This post was translated from Hebrew using AI (ChatGPT 5 Thinking), so there may be inaccuracies or nuances lost. If something seems unclear, please refer to the Hebrew original or contact us for clarification.

In the previous column I discussed the leniency of “two majorities” (trei rubei) in cases of agunot, as an example of the halakhic meaning of multiplying probabilities. I opened that column with a decision tree that represents a situation of safek sefeka (double doubt), because this is the fundamental discussion of multiplying probabilities in halakhah. In this column I return to safek sefeka itself, and we will see that several of the ideas presented there are relevant here as well. By some providence, on the very day I posted the previous column I received a question that dealt with a “reversible” safek sefeka (mit’hapech), which is almost the essence of the multiplicative property in the laws of safek sefeka. As I wrote to the questioner, I will address that as well here, and along the way I will explain why I disagree with the Shach whom he cited (though, as I will note, R. Akiva Eiger agrees with him).

What Is a Safek (Doubt)?

Halakhah by its very nature assigns norms to factual states: in a given factual state X, we must do or refrain from doing Y. To act according to halakhah we must know the factual state precisely, and also the normative directive that pertains to it. We can represent this picture as follows:

Diagram A: A regular ruling

The circle depicts the state before me, X, regarding which I am supposed to know what to do, and at the end of the branch appears the halakhic directive pertaining to it, Y. Halakhah is the line that leads from the factual state to the norm.

The problem of doubt arises in situations where we lack clear knowledge of the state X (a doubt in reality) or of the normative directive that pertains to such a state (we do not know what Y is; this is a sefeika de-dina, a doubt in law). These are states of uncertainty, and we must know how to act in them. Here the laws of doubts apply. In any case of doubt we have several possibilities and do not know which one is correct. For simplicity we will deal here only with doubts between two possibilities (which is the usual case). If the two possibilities before us have different weights, this is the law of majority (rov), discussed in the previous column. If their weights are equal—this is a state of (balanced) doubt and the laws of doubts apply. The main rule here is: a doubt in Torah law is treated stringently (safek de-oraita lechumra) and a doubt in rabbinic law is treated leniently (safek derabbanan lekula).

The decision tree of a state of doubt (I will not distinguish here between a sefeika de-dina and a doubt in reality) is as follows:

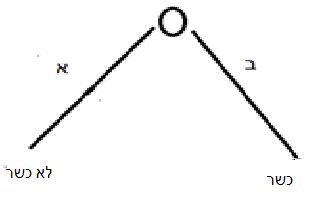
Diagram B: A regular doubt

The top circle represents the factual state about which I need to decide (the nature of the piece of meat before me). In a factual doubt I have two equally weighted possibilities: A – chelev (forbidden fat), B – shuman (permitted fat). To each I assign a probability of 0.5 (50%). As we saw above, the path from the question (the state) to the answer (the normative directive) is a route along the decision tree. Each branch is in fact a case like Diagram A, except here we have two possible branches. Note that even if the doubt were in law (in the directive), the diagram would be the same, only the top circle would be the state and the branches would depict a doubt between two rulings (and not between two factual states). But the analysis is identical, and therefore henceforth I will refer to a factual doubt.

When I know that it is chelev, I go from the top circle in Diagram B along branch A—at whose end there is an answer: not kosher. If I know it is shuman, I go along branch B—and at the end there is the opposite answer: kosher. Each of these is a simple tree like Diagram A. But if I do not know which of the two possibilities is correct, I assign each branch a probability of 0.5 (50%). Now there is a 50% chance the piece is kosher and a 50% chance it is not. Because of the laws of doubts, in a Torah law I must be stringent, while in a rabbinic law I may be lenient.

Important Reminder: Positive vs. Negative Doubt

In the previous column I noted that there can be two different types of doubt: a positive doubt and a negative doubt. A positive doubt is one that assigns equal weight to the two possibilities based on information I have about them. For example, with a fair coin there is equal chance of “heads” and “tails,” because I know the coin is fair. But there is also a negative doubt, a case where I assign equal weight to the two possibilities due to lack of information (ignorance). For example, a coin about which I have no information regarding its makeup (whether it is fair or not, and how it is biased). Here too, if I had to bet I would assign equal probabilities to the two possibilities (since I have no way to prefer one over the other), and therefore I also view this situation as a balanced doubt. But the balance here is the result of ignorance (and not of information). Therefore this is a negative doubt. In Shev Shema’tata 1:18 this distinction is explicitly made (in explaining the Rivash).

Recall that in the previous column I noted a similar situation regarding majorities. There too there are cases where I have a numerical measure of the majority (80%, 55%, 99%, etc.), and then usually this is a positive majority (based on information). But in most cases I do not have such a numerical measure. At most I can say that this is a large or small majority (in the previous column I defined three kinds of majority: overwhelming, absolute, and regular). This is a negative majority, since it is not based on clear information. I have general information that the odds lean to one of the possibilities, but nothing beyond that.

What Is Safek Sefeka (Double Doubt)?

What happens if I have a doubt about the animal from which this piece of meat was taken? If from a pig—then it is not kosher even if it is shuman; if from a cow—then it is kosher if it is shuman, but if it is chelev then not. This is a case of safek sefeka, and its decision tree is the following:

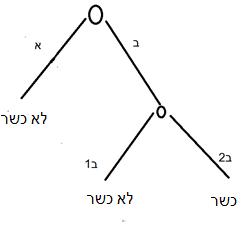
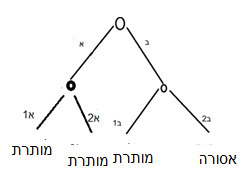
Diagram C: Safek Sefeka toward stringency

The top circle is the factual state before me, or the question: what is the piece of meat before me—chelev (A) or shuman (B)? The second circle is placed under the branch of shuman (B), at which point the second question arises (another node that also represents a doubtful factual state): is it cow fat (B2) or pig fat (B1)? As stated, if I have full information, I must traverse the decision tree according to my information. For example, if I know it is pig fat, the route is to the right at the upper node and to the left at the lower one. At the end of the route there is a clear outcome for such a case: not kosher. The same for cow fat (right, right: kosher). Chelev (left; and here it does not matter whether pig or cow—the result is not kosher).

What if I do not know the answers? Again I must do a probability calculation. There are three leaf nodes in our tree, but they do not all have the same probability. Every node along the route represents a balanced doubt (negative or positive).\[1] Therefore, as I proceed along a route, each passage through a node multiplies the result by 1/2. For example, a route that goes through two nodes (ending at B1 or B2) has probability 1/2 × 1/2 = 1/4. In contrast, a route that passes only one node (A) has probability 1/2. Thus there is a 1/4 chance it is cow fat, a 1/4 chance it is pig fat, and a 1/2 chance it is chelev (regardless of pig or cow). Therefore in such a case there is a 3/4 chance it is not kosher and a 1/4 chance it is. This is a safek sefeka toward stringency (most of the odds point to stringency, and one must be stringent).

It is important to understand that this is merely an example to illustrate the logic. Usually a safek sefeka is described by such a tree but toward leniency, i.e., a graph with three “kosher” outcomes at the bottom and one “not kosher” (where the chance is 3/4 to permit and 1/4 to forbid). Below we will discuss such an example from Ketubot. The reason safek sefeka is usually lenient is that if it were a safek sefeka toward stringency like ours, it would have no practical implications, since even a single doubt in de-oraita requires stringency; certainly when most of the odds point toward stringency one must be stringent.

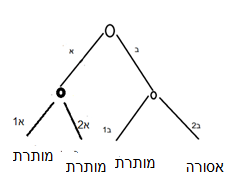
One could present the same decision tree in Diagram C in a different, fuller way:

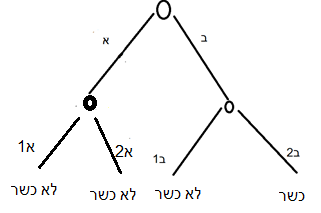
Diagram D: Safek Sefeka, full presentation

Here I presented the doubt of pig vs. cow also under the chelev possibility (A2 – cow, A1 – pig), even though there it makes no halakhic difference. The advantage of this presentation is that now each outcome has the same probability (because the path to each has two nodes). In this situation one need not calculate with multiplications; one can simply count the leaves and reach the result directly: there are three “not kosher” outcomes and one “kosher,” hence the chance is 3/4 toward stringency and one must be stringent.

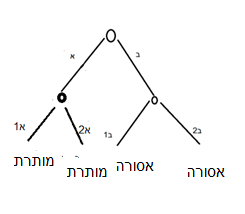
Note that if the distribution of outcomes were 2–2, as in the following drawing, it would not be a safek sefeka:

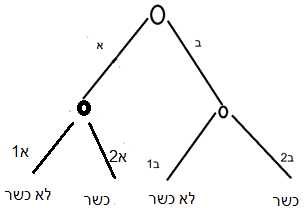
Diagram E: A safek-sefeka-like tree without multiplication, only parallels

For example, I have a doubt whether this is goat or cow, but in both there is a doubt whether it is chelev (forbidden) or shuman (permitted). Therefore here the chance it is not kosher is 1/2, and this is a single doubt rather than a double doubt. This is entirely parallel to the case of “two majorities” that is not a “majority of a majority” (ruba deruba) from the previous column. I explained there that here there is no multiplication, hence this is essentially a single majority. Likewise here there is no multiplication; thus this tree describes a single doubt, not a safek sefeka.

Safek Sefeka and Majority: A “Majority of Sides”

The commentators discuss why we allow ourselves to be lenient in a safek sefeka even in Torah prohibitions (see a survey, for example, here). Rambam’s view is that the rule “a doubt in Torah law is stringent” is itself rabbinic. According to him one could say that a safek sefeka is a rabbinic doubt and therefore we are lenient. But according to most Rishonim, who hold that “a doubt in Torah law is stringent” is itself de-oraita, the most reasonable explanation for leniency in safek sefeka is that it follows the rule of going after the majority. When we have a safek sefeka tree that favors leniency (three “kosher” possibilities), then most of the odds (0.75) are that it is kosher, and we follow the majority. This is indeed how the Rashba understands it (Torat HaBayit, Bayit 4, Sha’ar 1). The question is: why do other commentators not accept this? Seemingly there is a majority here, and the rule of majority could explain everything. One could press further: why do we even need the notion of safek sefeka if we already have the rule of majority? Consider a case of a positive doubt, i.e., where we have information that each doubt is truly 50%. In that case, in a safek sefeka there is a clear majority of odds toward leniency (75%), and then we would not need the law of safek sefeka at all; the regular rule of majority would suffice.

The conclusion that emerges is that the law of safek sefeka is relevant only to negative doubts. When the doubts are positive, there is only the rule of majority. In negative doubts there is a special novelty of the Torah that even though there is not necessarily a majority of probability, we may treat it as a majority. And indeed we saw in the previous column that in most cases of doubt (and of majority) we are dealing with negative doubts. In such a situation we do not know the probability of each of the two possibilities, and out of this ignorance we assume they are balanced. In such a doubt there is no necessity to say that there is truly a probability majority toward leniency, and therefore we need the laws of safek sefeka in addition to the laws of majority. In a safek sefeka there is one side versus three others, and we have no information about the true chance of each possibility (“side”), for it could be that the single side has a chance equal to or greater than the other three combined. But since we do not know each side’s probability, halakhah tells us to assume equal weight for each.

In a regular doubt we assume balance, and those are the laws of doubts: as if there is a 50% chance for each side. In a safek sefeka—which, as noted, applies only to negative doubts—we again count “sides.” Here there are three sides for leniency, and therefore we permit. In other words, we do indeed follow a “majority” here, but not the regular rule of majority of probabilities, since there is no such probability majority. Rather, it is a halakhic novelty that when there is no information we go by a majority of sides: in a regular doubt it is one side versus one, while in a safek sefeka it is one side versus three, and therefore we permit.

The Category of “Sides” Is Halakhic, Not Probabilistic

It is very important to grasp the logic (or illogic) underlying this picture. To that end we return to the example of chelev vs. shuman in pig vs. cow. The fact that in a regular doubt between cow and pig we assume there is a 50% chance for cow and 50% for pig is simply a rule. We have no indication that the doubt is balanced, but in the absence of other information that is our assumption. This is a negative doubt. Now we add another doubt—whether it is chelev or shuman—which is likewise a negative doubt. We have thus reached a safek sefeka (since we lack information about the distributions of both pig vs. cow and chelev vs. shuman), and as we have seen, we count sides and follow the majority of sides (which is not the regular rule of majority).

But in such a case there is no necessity to speak of four sides. The choice to split a safek sefeka and view it as four sides is somewhat arbitrary. We could just as well say there are only two sides: kosher or not kosher; that itself is a two-sided doubt, and in the absence of information we should assign equal chance to both—thus a stringent doubt. Likewise we could say there are three sides (as in Diagram C), and then the majority is 2/3 rather than 3/4. The assumption that branch A carries double the weight of the other two is based on a probabilistic perspective that lacks a true factual basis (this is a negative doubt). That is why I suggested the fuller presentation in Diagram D. There the safek sefeka has four sides, and then going by the majority toward leniency looks more natural without needing probabilistic assumptions about different weights of leaves. All paths—or their leaves—have equal weight.

Yet there are additional ways to define “sides.” Not only two or three as just seen; we could equally well split the decision tree into more sides (seven, ten, a hundred). For example, we could discuss whether it is a warted pig, a regular pig, or a giraffe; and on the permitted side, whether it is a Dutch or Australian cow, or perhaps a goat. We could debate whether it is the soft part of the chelev or the hard part, and so on. If we assign equal weight to every such side (absent information), we could reach any halakhic outcome one desires. Note this is not irrational statistically; it is no less reasonable than the choice to present a safek sefeka as a four-sided tree.

The conclusion is that splitting a negative safek sefeka into four sides is an arbitrary decision without factual or statistical basis. In positive doubts such a division does have a probabilistic basis, but as we saw, in a positive doubt there is no need to enter the laws of safek sefeka, since there we have the usual rule of majority. In a safek sefeka we are always dealing with a negative doubt. It may look like a probabilistic calculation, but it rests on a non-probabilistic foundation. The division into “sides” in the given problem is a rule—that is, a halakhic consideration—and it underlies the subsequent probabilistic calculation. Once we have the sides, we assign them equal weight and then count them as if they were probabilities. The conclusion is that the division into sides is the crux of the discussion in the laws of safek sefeka, and that is a halakhic question, not a probabilistic one. But from here on, for our purposes it is a probabilistic calculation (similar to what we saw in the previous column regarding majority and “two majorities” in agunot).

This leads us to two rules in the laws of safek sefeka that are tied to the picture described thus far.

“When the Label of the Doubt Is One”

The Gemara in Ketubot 9a discusses the husband’s claim “I found an open orifice” (petach patuach matzati):

R. Elazar said: One who says ‘I found an open orifice’ is believed to render her forbidden to him.

The husband claims she is not a virgin, and if she had intercourse during the marriage she becomes forbidden to him and to the adulterer. R. Elazar says the husband is believed and she is forbidden to him. The Gemara asks:

And why? It is a safek sefeka! Perhaps \[the intercourse was] with him, perhaps not with him; and if you say it was with him—perhaps by coercion (ones), perhaps willingly (ratzon).

The Gemara’s question shows that in the claim of “open orifice” there is a safek sefeka: a doubt whether it happened during the marriage or not (if not, she is not forbidden), and even if it did—another doubt whether coerced or willing (she is forbidden only if willing during the marriage). If so, the husband should not be able to forbid her, since in a safek sefeka we are lenient and rule she is permitted. This is difficult for R. Elazar.

The Gemara resolves this in two ways:

It is needed—in the case of a priest’s wife. And if you wish, say: in the case of an Israelite’s wife where her father accepted betrothal for her when she was less than three years and a day old.

If she is a priest’s wife there is no difference between coercion and willingness (in both cases she becomes forbidden to him), hence there is only one doubt. A second answer: her father accepted betrothal when she was under three years old; in such a case she could not have had intercourse before the betrothal because her hymen would regrow.

On Tosafot s.v. “ve’i ba’it eima” there, they ask:

If you say—there is still a safek sefeka: perhaps coerced, perhaps willing; and if willingly—perhaps when she was a minor, and the seduction of a minor counts as coercion, etc.

Tosafot challenge the second resolution (the father accepted betrothal before age three), that there is still a safek sefeka: perhaps coerced, perhaps willing; and even if willing—perhaps it was when she was still a minor, and the seduction of a minor counts as coercion (for she lacks full consent).\[2]

The tree in question is similar to Diagram C or D (which is a full presentation of the same safek sefeka as C), but this time toward leniency (there are three possibilities of permission):

In our case the first doubt is coercion (A) vs. willingness (B); and if it was willingness, there is a further doubt whether she was a minor (B1) or an adult (B2). If we use the full presentation of Diagram D (where the second doubt appears also under option A), we get four leaves: coerced minor (A1), coerced adult (A2), willing minor (B1), and willing adult (B2). In three of them she is permitted, and in one she is forbidden.

Tosafot answer:

One can say: the category (‘name’) of coercion is one.

The case of willingness while a minor (B1) and the cases of coercion as an adult or minor (A1 and A2) are the same possibility. All these are cases of coercion, and “the label of coercion is one.” Therefore we actually have only a single doubt, like Diagram B above (option A represents the three coercion possibilities): coercion or willingness:

Hence we must forbid her as in an ordinary doubt.

The commentators take this Tosafot principle and turn it into a general foundation in the laws of safek sefeka: when the “label of the doubt is one” (shem safek echad), we view all such possibilities as a single possibility. This is, of course, based on what we saw above, that the division into possibilities (“sides”) is a halakhic matter rather than a probabilistic one. Tosafot’s halakhic consideration is that all possibilities that lead to coercion should be considered one possibility.

But if we merge all the lenient possibilities into one, does safek sefeka disappear from the world? Seemingly any safek sefeka could be collapsed into a single doubt. For example, in the original double doubt (coercion vs. willingness; during the marriage vs. not), one might say that the three lenient possibilities (coercion during marriage, not during marriage, willingness not during marriage) bear a single “name”: they all yield permission. “The label of permission is one.” But this is mistaken. Tosafot’s rule concerns the rationales, not the ruling. When the rationales are of one kind (=coercion), they are one “name.” But when the outcome is the same (=permitted), that does not unify them into a single side. When we speak of coercion, that is a rationale for why the woman is not forbidden, and different forms of coercion are the same rationale: coercion.

This is like what we saw above: one does not split the doubt into additional artificial sides (e.g., warted pig vs. regular pig). If we separated between seduction of a minor (counted as coercion) and coercion of an adult, we could equally split coercion into many different possibilities: coercion by holding hands, with or without tying, deception, etc. All these are types of coercion, and there is no reason to make them separate sides: “the label of coercion is one.” In contrast, when the norms at the end of several paths are similar (all “permitted,” or all “kosher,” etc.)—we obviously do not unify them. If we did, safek sefeka would not exist.

From this you can understand that Tosafot’s principle, “when the label of the doubt is one,” follows from the earlier description (similarly noted by R. Z.N. Goldberg in his article here). Obviously if the doubts are positive, none of this discussion is relevant. First, we saw that in such cases we do not enter safek sefeka at all; the law is determined statistically. Second, in positive doubts there is a natural division of sides and we do not need to weigh their labels: a “side” in a positive doubt is whatever has a 50% chance. If the sum of several sides adds up to 50%, they will be joined regardless of their “name.” If, say, I know that the chance that the woman was seduced as a minor or coerced is 50% and the chance that she did so willingly as an adult is 50%, then I have a balanced doubt, and I do not care that the first side is a combination of several sides. I have a balanced doubt because in fact there is 50% that she is permitted and 50% that she is forbidden. That is a statistical, not a halakhic, consideration. But, as stated, for our purposes we are dealing only with negative doubts, and there we need the rules of safek sefeka and the labels of the doubts determine the relevant sides.

Reversible Safek Sefeka

Several Rishonim and Acharonim wrote that in the rules of safek sefeka there is an additional principle: a safek sefeka must be “reversible” (mit’hapech). In their view, a safek sefeka that is not reversible is not a safek sefeka. I must note that this rule is not universally accepted (the Shach embraces it enthusiastically, but the Maharit and the Pri Ḥadash disagree), yet it is accepted by many. Here we will examine it according to those who require it.

One source is in Tosafot Yeshanim on Ketubot 9b. By way of preface: a woman who marries not as a virgin has a ketubah of a maneh (100), not 200. Therefore in the husband’s claim of “open orifice” there is a discussion both of the prohibition (whether she is forbidden to her husband) and of money (the ketubah amount). In Tosafot Yeshanim s.v. “i le-meitav,” they infer from the Gemara that regarding money the husband would be believed to reduce her ketubah. They immediately ask why the husband is believed to cause her a monetary loss—it is a safek sefeka: perhaps he is expert in diagnosing an open orifice, and even if yes—perhaps coercion, perhaps willingness. Essentially there is a doubt whether she is in fact be’ulah (since perhaps he is not expert and she is in fact a virgin), and if be’ulah there is a doubt whether coerced or willing. Tosafot and the commentators answer in various ways.

But Tosafot Yeshanim resolve as follows:

There are those who say that here it is not considered a safek sefeka, because one cannot reverse it and first say “perhaps coerced, perhaps willing,” and if willingly “perhaps …,” and therefore it is treated as a single doubt.

They argue that a safek sefeka must be such that one can switch the order of the nodes in Diagrams C and D. For example, in the earlier example one may first doubt whether during the marriage or not, and then, if during the marriage, doubt whether coerced or willing; and one can reverse the nodes—first doubt coercion vs. willingness, and then, if willingness, doubt whether during the marriage or not. Only when the nodes can be swapped is it a safek sefeka. If they cannot be swapped, it is treated as a single doubt and we are not lenient. In the case of Tosafot Yeshanim this is a non-reversible safek sefeka, for one cannot first doubt coercion vs. willingness and then doubt whether he is expert in diagnosing “open orifice”; if he is not expert, then she is a virgin and there is no room to doubt how she had intercourse (coercion or willingness). As noted, commentators and posekim broadened this to be a general principle in the laws of safek sefeka.

The logical explanation for this rule is unclear. The Rema mi-Pano suggests that since the sides of the doubt can be raised only in one order and not the other, we have a doubt about whether to present the doubts in the first order (and be lenient) or in the second (and be stringent). Since this itself is a de-oraita doubt, we must be stringent. But this explanation is not compelling for at least two reasons:

• That itself generates a safek sefeka: whether to present the doubts in this order or the reverse, and if we present them in the first order there still remains the single remaining doubt. Why not be lenient in such a safek sefeka? One can wonder similarly about those Rishonim who hold that “a de-oraita doubt is stringent” is de-oraita: why not be stringent also in a safek sefeka, since that itself is a de-oraita doubt (a doubt that perhaps we have a case requiring stringency)? Acharonim discuss this (see, e.g., Sha’arei Yosher, Sha’ar 1, chs. 3 and 19). It can be explained that if we have a doubt whether to raise a doubt, we are not obligated to raise it; the rule of stringency in de-oraita doubts does not obligate us in that meta-doubt.
• It should suffice that there is one order of doubts that creates a double doubt to be lenient. Why should it matter that there is another order where the ruling would be stringent?! It is like in a kal va-ḥomer argument: it suffices to formulate it one way to prove the ruling, even if the “vertical” formulation was refuted (see in column 537).

We will return to explaining this rule after discussing the relationship between the two rules.

The Relationship Between the Two Rules: Reversibility and “Single-Label Doubt”

The posekim cite another example of a non-reversible safek sefeka, regarding a nick (pegimah) in a shechitah knife (see the Shach in the rules of safek sefeka, no. 13, in the name of the Agur). From Chullin 10b it emerges that one who slaughtered an animal and later found the knife nicked—the slaughter is invalid and the animal is a nevelah. Some Rishonim ask why we do not permit the animal by a safek sefeka: perhaps the knife nicked during the slaughter, perhaps after (when it hit the spine); and even if it nicked during the slaughter—perhaps it was after most of the neck had already been cut (and then the slaughter is not invalidated). The answer: this is a non-reversible safek sefeka, since if we begin with the second doubt—whether the nick occurred before cutting most of the neck—we obviously cannot then continue and say that even if it nicked before most of the neck, perhaps it nicked after the slaughter.

In this example one can also argue it is a “single-label doubt.” Whether it nicked after the slaughter or after most of the slaughter—the single label is: it nicked after the stage at which the slaughter was already valid. Indeed, to the same extent we could add many more sides: perhaps it nicked after 51%, after 54%, after 80%, after 98%, and entirely after the slaughter. All these are the same side: the knife nicked at a stage where the slaughter remains valid.

This hints to the question of many scholars: why see these as two different rules at all? On the face of it, “single-label doubt” and “non-reversible safek sefeka” are one and the same rule. To strengthen this, see here that R. Akiva Eiger understood Tosafot’s answer on Ketubot 9a (“the label of coercion is one”) as meaning that it is a non-reversible safek sefeka. If we start with the doubt of coercion vs. willingness, we cannot continue and say: if willingly, perhaps as a minor—for the act of a minor is considered coercion, and thus that branch collapses back into coercion.

From these two examples one could infer that the two rules are identical. Many indeed tend to see them as two faces of the same rule. If so, there is no question why a safek sefeka must be reversible: the explanation would be the same as for “single-label doubt,” namely, reversibility is required so that we truly have distinct sides of doubt that create a majority of sides toward leniency (so argues R. Shlomo Levi at the opening of his article; he then rejects it). However, as we shall now see, this is apparently not correct.

Already in Tosafot’s Ketubot example we can see the two rules are not identical. Unlike R. Akiva Eiger’s assumption, one certainly can present the doubts in the reversed order: start with willingness vs. coercion, and on the willingness branch further doubt minor vs. adult. True, as far as the ruling goes, willing minor counts as coercion, so at the end of the paths both sides yield “permitted” (see above, Diagram D, where under branch A there is a split whose two sides have the same ruling). At most one could claim there is no point to raise the doubt because “the label is one” (both are effectively coercion).\[3] In other words, Tosafot’s Ketubot case is an example of a reversible safek sefeka—but the label of the doubt is one (all the rationales for leniency are the same rationale: coercion), and therefore we are stringent. This is not like the shechitah case, where one cannot raise the second doubt at all in reversed order—there it is both non-reversible and a single-label doubt. I will note here that also in the question I mentioned at the start of the column, the Shach’s example of a non-reversible safek sefeka in shechitah is cited, and he argues it is non-reversible because the second doubt makes no practical difference on the first branch. But as I have argued here, the lack of practical difference does not make it non-reversible. For a structure to count as non-reversible one must be unable to raise the second doubt at all (as in Tosafot Yeshanim’s Ketubot case).

Thus far we have seen that there can be a case where the label is one but the doubt is reversible (Tosafot Ketubot). Is there a case where the doubt is non-reversible but the label is not one? Shechitah is not such a case, because we saw there it is both non-reversible and a single-label doubt (the doubt is whether it nicked after the slaughter was already valid). But the Tosafot Yeshanim case in Ketubot 9b—the first case we saw of a non-reversible safek sefeka—there the label does not appear to be one. If the husband is not expert—the leniency stems from the fact that she was not intimate at all. But if he is expert and she nevertheless is leniently ruled because it was coercion—then the leniency stems from a different rationale: coercion. These are two distinct “names” of lenient sides that lead to the same norm. We saw above that “single-label doubt” applies to the rationale (the sides), not to the norm itself.

From what we have seen it clearly emerges that these two rules are not identical, and in fact they are independent: there is a safek sefeka where we are stringent because it is non-reversible even though the labels of the lenient sides are not one (Tosafot Yeshanim in Ketubot 9b), and there is a safek sefeka where we are stringent because the labels are one even though it is reversible (Tosafot on Ketubot 9a). So it follows also from the fact that there are positions which do not require reversibility, but do accept that when the label of the doubt is one it is not a safek sefeka.\[4]

I reiterate that the “single-label doubt” rule is logical and compelling as explained above. But if indeed we are right that these two rules are independent, we must still seek a separate explanation for the rule that requires reversibility. We have not yet found a satisfactory explanation.

Explaining the Rule of Reversible Safek Sefeka

We have seen in the previous and current columns that contrary to common assumptions, the rules of doubt and majority are rooted in a probabilistic perspective. The rules of safek sefeka are needed only when dealing with negative doubts (and these are the overwhelming majority of cases and examples in halakhah). In such cases we have no actual numbers describing the probabilities, and the decision to treat such a doubt as balanced is a halakhic decision, not a probabilistic one. But from that point on, for our purposes we view it as a probabilistic question described by a tree in which each node is a balanced (negative) doubt, and we must decide using probabilistic “glasses.” The chance of each outcome is the product of the probabilities at the nodes along the way. If so, we must examine a safek sefeka tree and ask what it means for it to be non-reversible. I can suggest two explanations.

First Explanation: Between Counting Sides and Probability

The first explanation follows the Rema mi-Pano mentioned above, but in a slightly different conceptual frame. Our starting point is that we are dealing with negative doubts. If so, we are essentially counting sides, not probabilities. The foundational rule that underlies leniency in safek sefeka is that a majority of sides is also a majority, even though it does not necessarily indicate a majority of probability. In a regular doubt there is one side each way, and although we have no way to examine whether there is really 50% each way, halakhah tells us to treat it as balanced and be stringent (in a de-oraita). In a safek sefeka we have three sides for leniency versus one for stringency, and therefore we go after the majority of sides and are lenient. What happens in a non-reversible safek sefeka?

The Rema mi-Pano suggested that in such a case we doubt whether to present the order of doubts in a way that yields a safek sefeka (and then one may be lenient), or in the reverse order that yields a single doubt (and then one must be stringent). He claimed this doubt itself is a de-oraita doubt and we must be stringent. But we saw above this is problematic. Here I propose a small variation. Let us view this as a doubt whether to draw a decision tree of a safek sefeka (i.e., three lenient sides vs. one stringent), or of a regular doubt (then there is one lenient and one stringent side), which for the sake of comparison we will depict as two leniencies vs. two stringencies (a more detailed presentation—akin to Diagram D above).

To illustrate, take the case of a non-reversible safek sefeka that is not a single-label doubt (this is the interesting case to explain)—namely Tosafot Yeshanim’s case in Ketubot 9b: doubt whether he is expert in diagnosing “open orifice” or not; and if expert—doubt coercion vs. willingness. In such a situation we have two ways to draw the structure. The first is to present it in the order described, yielding the following tree:

Here A represents the possibility that he is not expert (i.e., the orifice was not open), in which case the coercion/willingness question does not arise and she is permitted. B represents the possibility that he is expert (i.e., the orifice indeed was open), and then it depends on coercion (B1) or willingness (B2). There are three lenient sides and one stringent.

The second option is to reverse the order and begin with coercion vs. willingness. We saw that in such a case we cannot continue and raise the doubt of expertise (since the first doubt assumes the orifice indeed was open). Therefore here we get a single doubt (coercion vs. willingness). We will represent it too as a “double” tree, but the norms at the bottom are equally split between leniency and stringency:

Here A represents coercion—in any case she is permitted; B represents willingness—in any case she is forbidden. There is no real possibility of “expert” (1) vs. “not expert” (2); I split each branch merely to keep the basis of comparison to the previous tree identical.

I now suggest, following the Rema mi-Pano, that we treat these two trees as two balanced options; therefore we must count all the leaves at the bottom of both. We then have eight possibilities, each of probability 1/8 (and not four of probability 1/4 as in a regular safek sefeka). We get a total of five lenient possibilities and three stringent ones. There is a majority of lenient sides, but smaller than in a regular safek sefeka (here 5/8 vs. 3/4). Now we must recall that we are comparing sides, not probabilities, for this is a negative majority (we cannot quantify the chance she was intimate before or after, or whether he is expert). But we saw that a majority of sides does not necessarily reflect a probabilistic majority, and only halakhah instructs us to treat it as an indicator of a probabilistic majority. My proposal is that, in order to accept a majority of sides as a probabilistic majority, halakhah requires a decisive majority of sides—at least 3/4 (or 6/8). If so, then a smaller majority of sides, e.g., 5/8, is insufficient, because there is a concern that there is no probabilistic majority, and therefore in a de-oraita prohibition we do not rely on it.

This is very similar to the explanation I proposed in the previous column for “two majorities.” There I explained that since this is a negative majority and we have no way to measure the probability numerically, we demand multiplication to ensure there is an absolute majority probability. The same, in essence, is the proposal described here for safek sefeka. This could be a possible explanation for why a non-reversible safek sefeka is treated as a single doubt—i.e., we cannot be lenient there.

But on further reflection this analysis is unconvincing. The reversed order ignores entirely the possibility that she was not intimate at all—i.e., that the husband simply erred because he is not expert. But clearly that is a possibility; it does not appear on that tree only due to the limitations of the description. It is therefore not reasonable to treat that tree as a balanced option alongside the regular safek sefeka tree that does present all possibilities. The tree that faithfully represents the case is only the regular one. The other is fictitious and there is no reason to account for it. Therefore there is no point in counting both trees’ leaves as if they were two possible descriptions.

The conclusion is that only the regular tree correctly depicts the case in such situations. The other tree is not genuine and we need not consider it. Still, such a tree has the property of being non-reversible, and apparently that is what prevents us from relying on it toward leniency. We must now seek an explanation for why non-reversibility weakens the case for leniency.

Second Explanation: Dependence Between Events

This explanation starts from the premise that although each node-doubt is not truly a balanced probabilistic doubt (that balance is a methodological assumption, since this is a negative doubt), from there on we view it as a probabilistic calculation. The crux of my proposal lies exactly here. In probabilistic calculations, if the order of occurrence matters, that indicates statistical dependence between the events.

Suppose we are discussing SIDS (Sudden Infant Death Syndrome). The chance that infant A will die of SIDS is P(A), roughly 1/8,000. What is the chance that two infants will die of SIDS? If the two events are independent, the chance is the product: P(A) × P(B). But if the two infants are from the same family, there may be a genetic factor affecting infant mortality; therefore, if we have seen that one infant died, the chance the second will die is higher. This is a situation of dependence between the two events (there is a factor affecting both). In such a case, the chance that both will die is not the product of each one’s probabilities (that holds only when there is no dependence), but P(B|A) × P(A), where P(B|A) is a conditional probability. If there is dependence between events A and B, it means the chance that B will occur, P(B), differs from the chance that B will occur given that A occurred—P(B|A). In our case, the conditional probability is larger than the absolute probability P(B); hence the product is larger as well. The conclusion is that if there is dependence between two events, the probability of the second changes (here—increases) if the first occurred.

Let us now return to a non-reversible safek sefeka. For the woman to become forbidden, two events must occur: (1) she is not a virgin (which is only if the husband is expert in “open orifice” and he diagnosed that she is indeed not a virgin); (2) that open orifice is the result of intercourse willingly, not by coercion. What is the chance that both will occur (that she is a be’ulah and that the act was willing)? Seemingly it is the product of the chances of each event: P(A) × P(B). But that is only when the safek sefeka is reversible, i.e., when there is no dependence between the events. If the order matters—i.e., event B can occur only if event A has occurred—this means there is dependence. In such a case, the chance that she is forbidden is P(B|A) × P(A). But, as noted, where there is dependence the conditional probability can be larger than the absolute probability P(B). It may also be smaller (there are such dependencies), but it may be larger.

The conclusion is that if the safek sefeka is non-reversible, there is dependence between the events (the nodes in the tree), and therefore the chance that the woman is forbidden could be larger than we thought. In such a case we lack certainty that the chance she is forbidden is small enough—or even that there is a majority chance she is permitted. Therefore, in such a safek sefeka we do not permit the woman. This is a possible probabilistic explanation for why a non-reversible safek sefeka does not yield leniency.

Two Reasons for Non-Reversibility: Substantive and Statistical

When we consider the example we have been using (doubt about the husband’s expertise and doubt about willingness vs. coercion), it seems this explanation does not hold water. The inability to reverse the sides of the doubt is not due to statistical dependence but to the substantive content of the events. In short, it does not appear that the chance of willingness is truly greater because of non-reversibility. Whether the husband is expert does not change the ratio of chances between willingness and coercion; it merely enables us to ask the question (if she was not intimate at all, there is no point discussing willingness vs. coercion). Therefore, in this particular case, it is implausible to say that non-reversibility changes the probabilities. The non-reversibility stems from a substantive, not statistical, matter.

This is also why I disagree with the Shach and R. Akiva Eiger, who understood that if the second doubt makes no practical difference, this counts as a non-reversible safek sefeka. I argued here that, contrary to their view, so long as one can raise the second doubt at all, it is considered reversible. A safek sefeka that is non-reversible is only when one cannot raise the second doubt at all. You can now understand why: non-reversibility has significance only if it indicates statistical dependence—that is, when the order of raising the doubts changes the probabilities of the factual possibilities (not the norms; I have emphasized several times that the doubts are about facts, not norms). In the Shach and R. Akiva Eiger’s cases, the probabilities of the facts do not change; only the norms change (their claim is that there is no halakhic practical difference between the different facts, but the facts themselves still differ). In light of the explanation proposed here, such a case is reversible.

The upshot is that only when the reason for non-reversibility is statistical does the leniency based on safek sefeka become more precarious. But regarding a safek sefeka that is non-reversible (in the facts, not in the law), even if the reason is not statistical dependence, it may be that because such a structure could exhibit dependence between events, halakhah sets a general rule: in such a safek sefeka we do not rule leniently. Thus, for non-reversible doubts, we nullify, in principle, the leniency of safek sefeka. From here on we do not inquire whether the non-reversibility points to statistical dependence or not—lo pelug.

Still, it is clear there must be cases where non-reversibility is due to statistical dependence; otherwise the entire approach has no meaning. If there indeed are such cases, we can say that we nullify the laws of safek sefeka when it is non-reversible, even if in the given case it does not stem from dependence. Are there truly such examples? Consider again the safek sefeka in Chullin regarding the shechitah knife. We saw it is non-reversible (and also single-label), and there non-reversibility indeed seems to arise from dependence between events. If I know the knife nicked before most of the slaughter, then it certainly did not nick afterward. As I move forward on the time axis, I leave behind everything that lies after the given time point. In such a case, non-reversibility appears to indicate statistical dependence. But, as noted, this is a non-reversible safek sefeka that is also a single-label doubt. The question is whether there is a case of a non-reversible safek sefeka that is not single-label and in which the non-reversibility stems from statistical dependence. For the proposed explanation to hold, it would be best to find such a case (otherwise the rule of reversibility is superfluous, for we already have an explanation for “single-label doubt,” and that certainly exists). At the moment I cannot think of an example, but I see no reason one should not exist.

\[1] It must be balanced; if it is not, the laws of majority apply. That was the subject of the previous column.

\[2] This assumes that the marital intercourse occurred after she reached bat mitzvah. That is, between the betrothal (before age three) and the marriage, more than nine years elapsed.

\[3] Indeed, R. Akiva Eiger ultimately rejects this explanation, for according to it even if she were betrothed under age twelve (not only under age three) we would have to forbid, since it would still not be a reversible double doubt by the same logic. This proves that the two rules are not identical.

\[4] So concludes R. Shlomo Levi in the cited article.