משמעותו של רוב: האם הרוב צודק? (טור 69)
בס”ד
בטור 66 עסקתי בשאלה האם הרוב קובע. המסקנה היתה שבדמוקרטיה כן, והסברתי זאת בכך שהרוב הוא מדד סביר כדי לקבוע את דעת הציבור בכללותו. כנגד ההצעה האפלטונית של שלטון הפילוסופים, כלומר מתן משקל יתר לאנשיםם חכמים, טענתי שבדמוקרטיה לא מחפשים החלטה נכונה אלא החלטה שמשקפת את רצון הציבור. השאלה האם הרוב הוא קריטריון טוב לקבל החלטה נכונה נותרה פתוחה, יען כי הליכה אחר הרוב בדמוקרטיה לא תלויה בה (הולכים אחרי הרוב בין אם הרוב צודק ובין אם לאו). כפי שהבטחתי שם, כעת אני מגיע לדיון בשאלה השנייה: האם הרוב צודק.
כאמור, ההנחה של אפלטון היתה שקבלת החלטות של מדינה אמורה לחתור לאמת, ובתוך כך הוא מתמודד מול האינטואיציה שהרוב הוא מדד לאמת. טענתו היתה שמיעוט חכמים מגיע קרוב יותר לאמת מאשר הרבה טיפשים, ולכן ממליץ על שלטון הפילוסופים. האם האינטואיציה הדמוקרטית אכן שגויה? האם באמת יש אלגוריתמים טובים יותר מאשר הליכה אחר הרוב כדי להגיע לאמת? מדובר על הקשרים שבהם מטרת ההחלטה היא האמת, כמו בהחלטה מקצועית כלשהי (שופטים, דיינים, החלטה מדעית או אסטרטגית כלשהי וכדומה). בנוסף, לפחות לצורך הדיון אניח כאן שקיים סוג של חכמה או כישורים ספציפיים שרלוונטיים להחלטה הנדונה.
מה המידע שיש לנו על המתדיינים?
התשובה לשאלה זו אינה פשוטה כמובן, והיא תלויה במידע שיש לנו על המתדיינים. אני מניח שנסכים שבשאלה שדורשת ידע ומיומנות (כמו שאלה מדעית), מעט מומחים יגיעו לתשובה טובה יותר מאשר קהל רחב של הדיוטות.[1] ומה אםם יששש מחלוקת בין מומחים? האם במקרה כזה הרוב הוא מדד לאמת? בעל ספר החינוך טוען שגם במקרה זה התשובה היא חיובית. במצווה עח (מצות “הטיה אחרי רבים”, בבית דין) הוא כותב:
ובחירת רוב זה לפי הדומה הוא בששני הכיתות החולקות יודעות בחכמת התורה בשוה, שאין לומר שכת חכמים מועטת לא תכריע כת בורים מרובה ואפילו כיוצאי מצרים, אבל בהשוית החכמה או בקרוב הודיעתנו התורה שריבוי הדעות יסכימו לעולם אל האמת יותר מן המיעוט. ובין שיסכימו לאמת או לא יסכימו לפי דעת השומע, הדין נותן שלא נסור מדרך הרוב. ומה שאני אומר כי בחירת הרוב לעולם הוא בששני הכיתות החולקות שוות בחכמת האמת, כי כן נאמר בכל מקום חוץ מן הסנהדרין, שבהם לא נדקדק בהיותם חולקין אי זו כת יודעת יותר אלא לעולם נעשה כדברי הרוב מהם, והטעם לפי שהם היו בחשבון מחויב מן התורה, והוא כאילו ציותה התורה בפירוש אחר רוב של אלו תעשו כל עניניכם, ועוד שהם כולם היו חכמים גדולים.
ראשית, חשוב להבין שבבית דין המטרה היא להגיע עד כמה שאפשר לאמת ההלכתית (זה לא רוב דמוקרטי שמבוסס על זכויות, אלא רוב בוויכוח בין מומחים שמנסים להגיע לתשובה הנכונה). בתחילת דבריו החינוך טוען שגם בין מומחים לאא תמיד נכון ללכת אחרי הרוב. גם בין אנשי מקצוע מיעוט חכמים מכריע את הרוב הפחות חכם. אבל כשהחכמה היא ברמהה דומה אז טענתו היא שהרוב הוא מדד טוב לאמת. אין זה אומר כמובן שהרוב תמיד צודק או בהכרח צודק, אלא שאם אנחנו מחפשים מדד אחיד ואפריורי לאמת, הרוב הוא מועמד טוב יותר מאשר המיעוט.
ומה לגבי מצב שאין לנו מידע על המתדיינים? או אם אין לנו מדדים ברורים לחכמה ולאינטליגנציה שלהם בתחום הנדון? לדוגמה, בחילוקי דעות בבית דין כשאין לנו מדד ברור לקבוע את מידת החכמה של הדיינים (אנחנו כולנו עמי ארצות, או פוסטמודרניסטים שלא מאמינים ביותר או פחות חכמה), האם במקרים כאלו נכון ללכת אחרי הרוב? דוגמה נוספת, כשיש חילוקי דעות בין קציני צבא באשר לדרך הפעולה הצבאית הנכונה. ברוב המקרים קשה לקבוע את דרגת החכמה הצבאית של המתדיינים (יכולים להיות רעיונות מבריקים לאחד שהאחרים לא חשבו עליהם. אבל במקרה שאף אחד לא משתכנע מהצעות זולתו ולא רואה בה פתרון מבריק לבעיה, קשה לקבוע מי חכם יותר שראוי לנהוג כהצעתו). האם במקרה זה נכון ללכת אחרי הרוב? אמנם גם במקרים כמו אלו יש מקום לקבוע שבהיעדר דרך ברורה להתקרב לאמת נאמץ את הרוב כקריטריון חלופי. לא כי הוא בהכרח יקרב אותנו לאמת אלא מפני שבהיעדר קריטריון אחר אך טבעי לאמץ אותו (למה? ככה! איזה קריטריון אחר יש לנו?!). אבל אם בכל זאת אנחנו רוצים למקסם את הסיכוי להגיע לאמת, האם רוב הוא אלגוריתם נכון?
השאלה הזאת תתברר מתוך דיון מעט שונה.
טיעונים מהתפלגות הדעות: דתיים-חילוניים וימין-שמאל
דוקינס בספריו כמו גם בכל מיני אתרים אתיאיסטיים למיניהם תמצאו מחקרים (בעיניי נכון יותר לכנות אותם סקרים) שמראים שבאופן ממוצע המשכילים נוטים לאתיאיזם והמאמינים הם פחות משכילים.[2] הוא הדין לגבי ימין ושמאל. עללל אף שהוצעו לכך כמה הסברים שלא קשורים לשאלה מה משני הצדדים נכון יותר, מאד נפוץ להציג את הנתונים הללו כטיעוןן לטובת השמאל והחילוניות. אם החכמים והמשכילים (לא אכנס כאן לשאלת היחס בין השכלה לחכמה) מצדדים בעמדה אחת והפחות משכילים וחכמים בעמדה אחרת, כי אז העמדה הראשונה היא כנראה נכונה. מה שמניחים כאן הוא שהמשכילים קולעים יותר לאמת. לכאורה זה מאד סביר, לא?
הערה צדדית: רלוונטיות של רוב ללא דיון
בכמה מקורות הלכתיים מובא עיקרון שיסודו בסברא, שאין חובה ללכת אחר הרוב אלא במקום שהרוב והמיעוט נשאו ונתנו ביניהם. כך למשל, כותב הרשב”א בתשובה (ח”ה סי’ קכו) לגבי בית דין, וגם בתשובה אחרת (ח”ג סי’ שד) בה הוא עוסק בהצבעה של נבחרי ציבור (הדברים חוזרים גם בשו”ת מהרי”ט ח”א סי’ צה ועוד). אמנם היה מקום להבחין בין הצבעה בשאלה הלכתית להצבעה בשאלה דמוקרטית, שכן הנימוקים עוסקים בעיקר בזכותו של המיעוט שדעתו תישמע. אבל גם בהצבעה הלכתית, שבה מחפשים את האמת ולא ביטוי לזכות של המצביע הבודד (ראה בטור 66 וכאן בתחילת דבריי), קיים אותו היגיון. אם המיעוט והרוב לא נשאו ונתנו ביניהם ולא שמעו זה את נימוקיו של זה, אזי אין משקל להחלטת הרוב. זו גם לא אינדיקציה לאמת. ייתכן שאם היו שומעים את נימוקי המיעוט הם היו משתכנעים. ואכן, מתוך כך כתבו כמה פוסקים[3] שבמחלוקת בין פוסקים שונים בשאלה הלכתית לא הולכים אחרי הרוב, שכן הם לא נשאו ונתנו זה עם זה (שלא כמו דיינים בבי”ד, שעליהם נאמר “אחרי רבים להטות”). כאן זו דוגמה מובהקת ל”הצבעה” שמטרתה היא האמת, ובכל זאת לא הולכים אחרי הרוב אם הוא לא ישב ודן עם המיעוט.
גם בסקרים מהסוגים שנדונו כאן יש להתחשב בכך שהצדדים לא באמת יושבים ודנים זה עם זה (בוודאי אין שם הקשבה של ממש לנימוקים השונים. להיפך, בדרך כלל יש זלזול הדדי מוחלט). במקרה כזה קשה להכריע לטובת הרוב רק מפני שהוא רוב. רק כאשר כל המידע, הטיעונים והנימוקים, חשופים בפני כולם ובכל זאת יש רוב לצד אחד יש לרוב הזה משקל כלשהו.
אך לצורך הדיון הבה נניח בכל זאת שכולם הגיעו למסקנותיהם אחרי ששמעו את כל הנימוקים ושקלו אותם. מה משמעותו של הרוב במצב כזה? האם הוא מהווה אינדיקציה כלשהי לאמת?
בדרך כלל המיעוט צודק
האינטואיציה האנרכיסטית הראשונית שלי היא שבכל ויכוח שני הצדדים טועים אלא אם הוכח אחרת. אבל גם אם שתי הדעות שמעומתות הן היחידות האפשריות (שאז לא ייתכן ששני הצדדים טועים) – כי אז בדרך כלל המיעוט צודק. היה לי אפילו טיעון חביב לטובת העניין. הרי סביר שיש פירמידת אינטליגנציה, כלומר שבקבוצת אנשים רגילה יש מעט חכמים והרבה יותר טיפשים. אז אם יש ויכוח ציבורי בנושא כלשהו שדורש חכמה, סביר להניח שהמיעוט הוא דעת החכמים והרוב הוא כנראה רוב האנשים (שכמובן בנוי מהטיפשים יותר). לכן בכל ויכוח נקודת המוצא צריכה להיות שהמיעוט הוא הצודק.
המסקנה היא שבוויכוחים אודות אמונה או ימין ושמאל, אם המיעוט שבין החכמים דוגל באמונה ובדתיות הוא כנראה צודק. בני משה הציע מודל מורכב יותר. הוא טוען שלפי התרשמותו ההתפלגות היא שארבעת העשירונים התחתונים הם ימין/דתיים, חמשת הבאים הם שמאל/חילוניים, והעשירון העליון הוא שוב ימין/דתיים. בסעיפים הבאים אציע מודל שיסביר את ההצעה הזאת.
שתי הנחות סמויות
במחשבה שנייה בבסיס האינטואיציה שלי יש שתי הנחות שלפחות אחת מהן לא סבירה: א. אנחנו מניחים כאן שההתפלגות היא הומוגנית (כלומר שהמיעוט מורכב ממיעוט החכמים והרוב מורכב מרוב הטיפשים). האם לא ייתכן ששתי המפלגות בנויות כל אחת מהן מחכמים וטיפשים? ב. התפלגות החכמה היא בצורה של פירמידה עם בסיס רחב וראש צר.
ההנחה הראשונה דווקא נשמעת לי סבירה למדיי. היא כמובן לא הכרחית, אבל לפחות בהיעדר מידע אחר הייתי מוכן לאמץ אותה. אם מדובר בהחלטה שדורשת חכמה, ויש לנו התפלגות של האנשים על ציר החכמה (המסוימת הזאת), כי אז סביר שבעלי אותה יכולת ואותה אינטליגנציה יגיעו לאותה תשובה. לכן אך סביר הוא להסיק שהמיעוט והרוב מפולחים לפי אינטליגנציה. תשאלו, מה לגבי ההתפלגות בין ימין ושמאל, דתיים וחילוניים, או סוציאליזם וקפיטליזם? ראשית, ייתכן שגם במחלוקות אלו זהו אכן המצב. שנית, אלו ויכוחים שתלויים גם בערכים ולא רק בעובדות וחכמה, ולכן שם פחות סביר להניח שהפילוח הוא דווקא לפי אינטליגנציה.
אבל ההנחה השנייה היא בעייתית בעליל. הרי כמו שיש מיעוט שהם חכמים מאד יש גם מיעוט קטן של טיפשים מאד. הרוב נמצא בתווך בין שני הקצוות הללו. במילים אחרות התפלגות החכמה אינה בצורה של פירמידה אלא משהו כמו גאוסיאן סימטרי. הנה דוגמה להתפלגות גאוסית של ציונים במבחן כלשהו:
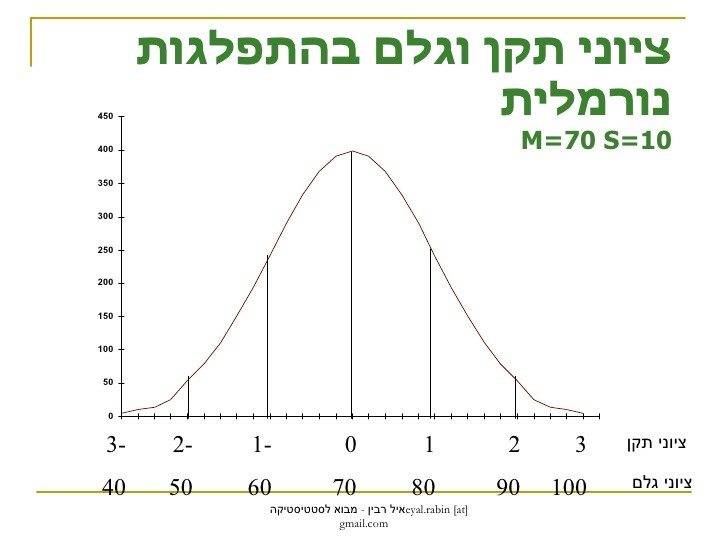
הציר האנכי מתאר את מספר האנשים שקיבלו את הציון שמסומן בציר האופקי.[4] הציון הממוצע הוא 70 (יש 400 איש שקיבלו אותו. במקרה הגאוסי הציון הממוצע הוא גם הציון שמתקבל במספר הגבוה ביותר של המקרים), וסביבו ישש התפלגות סימטרית של הציונים בקבוצה. רוב הנבחנים מקבלים ציונים שבין 60 ל-80 (סטיית תקן אחת ימינה ושמאלה מהממוצע), ומעטים מקבלים ציונים גבוהים ונמוכים יותר. ככל שהציון קיצוני יותר יש מספר קטן יותר של אלו שקיבלו אותו. אם נתייחס לגרף הזה כהתפלגות החכמה בין המתדיינים שלנו (עשינו להם מבחן אינטליגנציה וזו התפלגות התוצאות), תוכלו לראות מיד שיש מעט חכמים ומעט טיפשים, ועוד פחות חכמים מאד וטיפשים מאד. הרוב נמצאים במקומות טובים יותר או פחות באמצע.
אם כן, גם אם נאמץ את הנחה א, שההתפלגות היא הומוגנית ומפולחת לפי אינטליגנציה, נצטרך להניח שהמיעוט שייך לאחד הקצוות, והרוב הוא כל היתר. אם נניח שבוויכוח הצבאי 30% מהקצינים מציעים את דרך פעולה X ושאר ה-70% מציעים את Y, עדיין יש לנו שתי אפשרויות פרשניות: א. המיעוט הוא אלו שיקבלו ציון מעל 80 והרוב הוא כל אלו שיקבלו מתחת לזה. ב. המיעוט הוא אלו שיקבלו מתחת ל-60 והרוב הוא כל אלו שיקבלו מעל. אם כן, גם אם נאמץ את הנחה א השאלה האם המיעוט צודק או הרוב צודק (כלומר האם לעשות X או Y) נותרת פתוחה, וזאת בגלל שהנחה ב אינה נכונה. המסקנה היא שאמנם אין סיבה להניח שהרוב צודק, אבל מאידך גם אין סיבה להניח שהוא טועה. אז חצי תאוותנו האנרכיסטית בידינו. אבל אל חשש אנחנו רק באמצע הדרך.
גאוסיאן קטום
חשבו כעת על מצב בו הדיון נערך בין סטודנטים במחלקה לביולוגיה באוניברסיטה למשל. הנחה סבירה היא שטיפשים גמורים אין שם, שכן הם עברו סינון סביר בעת קבלתם ללימודים (מבחן פסיכומטרי וציון בגרות). משמעות הדבר היא שהגאוסיאן שלנו קטום מלמטה. מודל סביר יניח שהרכב הכיתה מתואר על ידי חלקו הימני של הגאוסיאן (החל מציון כלשהו ומעלה). במצב כזה יש לנו את מעט החכמים אבל אין את מעט הטיפשים. אמנם לא בהכרח שגדולי חכמי היקום נמצאים בכיתה הזאת, אבל ברור שהתפלגות האינטליגנציה שם לא נראית כמו בכלל האוכלוסייה. הסינון הוא כיווני (כלפי מעלה), והוא שובר את הסימטריה. התוצאה דומה להתפלגות הפירמידה שממנה יצאתי בשלב האנרכיסטי, ולכן לצורך הדיון אפשר להניח שמדובר בגאוסיאן קטום מלמטה. גם אם זה מודל פשטני עדיין ברור שההתפלגות במצב כזה כבר אינה סימטרית, ולכן המסקנה שבמקרה של ויכוח בין סטודנטים במחלקה לביולוגיה, או בוויכוח בין אנשי אקדמיה (בהנחה שגם שם יש סינון שקוטם את ההתפלגות מלמטה), המסקנה היא שהמיעוט צודק. בתוך אוכלוסייה ממוינת כלפי מעלה יש היגיון רב לטענה שהמיעוט הוא הצודק. לעומת זאת, באוכלוסייה שממוינת כלפי מטה הרוב צודק.[5]
יישום לסקרי ההשכלה-אמונה
כעת איישם את הדברים לטענות לגבי עדיפות השמאל והחילונים מבין המשכילים, ותראו איזו תוצאה מפתיעה מתקבלת. הטענה היסודית אינה שכל המשכילים הם שמאל חילוני וכל הלא משכילים הם ימין דתי, אלא שמבין המשכילים הרוב הוא שמאלי-חילוני ומבין הלא משכילים הרוב הוא ימני-דתי. כדי לנתח את התוצאות הללו ולהסיק מהן מסקנות, נתבונן תחילה בקבוצת המשכילים. זו מתוארת על ידי גאוסיאן קטום מלמטה, ולכן במקרה זה דווקא המיעוט צודק (כי בגאוסיאן כזה המיעוט הוא החכם יותר). רק אזכיר שמבין המשכילים המיעוט תומך בימין ואמונה. המסקנה היא שמניתוח התוצאות בין המשכילים נכון יותר להסיק לטובת התפיסה הימנית-דתית. כעת נעבור להתבונן בקבוצה השנייה, זו של הפחות משכילים. כאן הגאוסיאן קטום מלמעלה, ולכן בקבוצה כזאת דווקא הרוב צודק (כי הרוב הם בצד החכם יותר). אבל כאן הרוב הוא הימני-דתי, ולכן המסקנה היא שוב שהתפיסה הימנית-דתית היא הצודקת. כלומר משני צדי המשוואה עולה שהנתונים הללו מובילים דווקא למסקנה הדתית-ימנית ולא כפי שנוטים לחשוב במבט ראשון (ייתכן שהמבט הראשון הוא שמאלי-חילוני, כלומר פחות אינטליגנטי).
אפשר כמובן להתווכח על כמה וכמה יסודות בניתוח הזה, ואין ספק שיש בו מידה רבה של פשטנות (עד כדי גיחוך). אני בהחלט אצטרף לאלו שיצחקו על ניתוחים כאלה, ובעצם זו גופא מטרתי בכתיבת הדברים. ועדיין דבר אחד ברור: הסקת המסקנות מתוצאות הסקרים שהובאו למעלה (על היחס בין השכלה לאמונה) פשטנית הרבה יותר מהניתוח שעשיתי כאן. לכן די בניתוח הפשטני הזה להראות שהמסקנה השמאלית-חילונית ודאי לא יוצאת ואפילו לא נתמכת מנתונים כאלה. במילים אחרות, אם מישהו בכלל מנסה להסיק מהנתונים הללו מסקנה כלשהי (כאמור, לא מומלץ), אזי לכל היותר ניתן להוציא מהם את המסקנה הימנית-דתית. חזרנו אם כן פחות או יותר לטענתו של בני משה שהובאה למעלה.
הערה: זמן רב אחרי כתיבת ופרסום הטור, בשיעור שנתתי על הנושא של רוב (ראו שיעורי וידיאו, פ”ת, רוב, מתאריך 18.10.2018), קיבלתי מאריק פשדצקי הערה נגד הסברא שהעליתי לגבי זה שבד”כ המיעוט צודק. ההערה נכונה ולכן אני מתקן כאן.
הוא טען שגם אם נקבל את המודל של פירמידת כישרונות, או מצב של גאוסיין קטום (כלומר כשיש מעט חכמים והרבה טיפשים), עדיין הרוב צודק. אנחנו עוסקים בשאלה בינארית, שיש עליה תשובה של כן או לא. בניגוד להנחתי כאן, הטיפשים לא עונים את התשובה השגויה אלא תשובה אקראית. לכן בממוצע חצי מהם יענו נכון וחצי לא. לעומת זאת, מבין החכמים רובם יענו נכון. לכן סה”כ יהיה רוב לתשובה הנכונה. כמובן שאפשר לערער גם על זה, אבל ברור שהמודל הבסיסי שהצעתי כאן אינו נכון. צודק!
[1] בטור 62 נגעתי קצת בחכמת ההמונים, והסברתי מדוע היא לא רלוונטית לשאלות מהסוג שלנו.
[2] ראו כאן וכאן (סביב הערה 34) תיאור מאוזן יותר. מקורות נוספים לגבי אבולוציה ובריאתנות מובאים בהקדמה לספרי אלוהים משחק בקוביות ובהערה 2 שם.
בדיון כזה חשוב להבחין בין סקרים שמראים שהמאמינים הם פחות משכילים (או שהאתיאיסטים הם יותר משכילים) לבין סקרים שמראים שהפחות משכילים הם מאמינים (או שהיותר משכילים הם אתיאיסטים). לכיוון הקורלציה יש משמעות שונה לענייננו. בדיון שיבוא אני אניח תוצאות שמבטאות את אחוז המאמינים/האתיאיסטים לפי רמת ההשכלה ולא להיפך.
[3] ראה ש”ך חו”מ סי’ כה סקי”ט, ובנתיה”מ (חידושים) שם סקי”ח ובאורים שם סי’ כ ועוד הרבה.
[4] התיאור פשטני כי לא נתתי את הרזולוציה. נסו לחשוב כמה נבחנים היו בסך הכל ותראו שאין דרך לדעת זאת מתוך הגרף. אבל לצרכינו כאן זה מספיק.
[5] שאלה למחשבה: האם גם בכיתות של סטודנטים לביולוגיה צפויה להיות התפלגות ציונים גאוסיאנית (עם שני זנבות לשני הכיוונים)? אם כן, האם זה סותר את התיאור שנתתי כאן?

