משמעותן ההלכתית של מכפלות הסתברותיות: ב. ספק ספיקא (טור 613)
בס”ד
בטור הקודם עסקתי בהיתר של ‘תרי רובי’ בעגונות, כדוגמה למשמעותה של מכפלת הסתברויות בהלכה. פתחתי את הטור בעץ אפשרויות שמייצג מצב של ספק ספיקא, מפני שזהו הדיון היסודי במכפלת הסתברויות בהלכה. בטור הזה אחזור לעסוק בספק ספיקא עצמו, ונראה שכמה מהרעיונות שהוצגו בטור ההוא רלוונטיים גם כאן. משום מה (השגחה?), ממש ביום שבו העליתי את הטור הקודם הגיעה אליי שאלה שעסקה בספק ספיקא מתהפך, שזו כמעט תמצית המשמעות של תכונת המכפלה בהלכות ספק ספיקא. כפי שכתבתי לשואל, בטור הזה אעסוק גם בה, ובתוך דבריי אסביר מדוע איני מסכים לדברי הש”ך שהוא הזכיר (הגם שכפי שאזכיר גם רעק”א מסכים להם).
מהו ספק
ההלכה מעצם טבעה עוסקת בהצמדת נורמות למצבים עובדתיים: במצב עובדתי נתון X עלינו לעשות או לא לעשות Y. כדי לפעול על פי ההלכה עלינו לדעת את המצב העובדתי לאשורו, וגם את ההוראה הנורמטיבית שנוגעת אליו. ניתן לייצג את התמונה הזאת כך:
![]()
שרטוט א: דין רגיל
העיגול מתאר את המצב שבפניי, X, שלגביו אני אמור לדעת מה לעשות, ובקצה הענף מופיעה ההוראה ההלכתית הנוגעת אליו Y. ההלכה היא הקו שמוליך מהמצב העובדתי אל הנורמה.
בעיית הספק מתעוררת במצבים שבהם אין לנו ידיעה ברורה על המצב X (ספק במציאות) או על ההוראה הנורמטיבית הנוגעת למצב כזה (לא יודעים מהו Y. זהו ספיקא דדינא). אלו מצבי אי ודאות, ועלינו לדעת כיצד לפעול בהם. כאן חלים דיני ספיקות. בכל מצב של ספק יש לנו כמה אפשרויות שאיננו יודעים מי מהן נכונה. לצורך הפשטות נעסוק כאן רק בספיקות בין שתי אפשרויות (זה המצב בדרך כלל). אם ישנו משקל שונה לשתי האפשרויות שבפנינו, זהו דין רוב שנדון בטור הקודם. אם משקלן שווה – זהו מצב של ספק (שקול) וחלים כאן דיני ספיקות. ההוראה העיקרית בתחום זה היא ספק דאורייתא לחומרא וספק דרבנן לקולא.
עץ האפשרויות של מצב ספק (אני לא אבחין כאן בין ספיקא דדינא לבין ספק במציאות) הוא הבא:
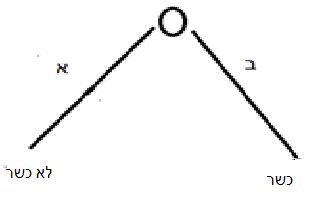
שרטוט ב: ספק רגיל
העיגול למעלה מייצג את המצב העובדתי שלגביו אני צריך להחליט (מה טיבה של חתיכת הבשר שבפניי). בספק עובדתי יש לי שתי אפשרויות שוות משקל: א – חלב, ב – שומן. לכל אחת אני מצמיד סיכוי של 0.5 (50%). כמו שראינו למעלה, הדרך מהשאלה (המצב) אל התשובה (ההוראה הנורמטיבית) היא מסלול על עץ האפשרויות. כל ענף כזה הוא בעצם מצב כמו שתואר בשרטוט א, אלא שכאן יש לנו שני ענפים אפשריים. שימו לב שגם אם הספק היה בדין (בהוראה), השרטוט הוא אותו שרטוט, אלא שהעיגול היה המצב והענפים כבר מתארים ספק בין שתי הוראות (ולא בין שני מצבים). אבל הניתוח הוא אותו ניתוח, ולכן מכאן והלאה אתייחס לספק עובדתי.
כאשר אני יודע שמדובר בחלב, אני בעצם הולך מהעיגול בשרטוט ב למעלה לאורך ענף א – שבקצהו יש תשובה: לא כשר. אם אני יודע שזה שומן, אני הולך מהעיגול לאורך ענף ב – ובקצה יש תשובה הפוכה: כשר. כל אחד משני אלו הוא עץ פשוט כמו בשרטוט א. אבל אם איני יודע מי משתי האפשרויות נכונה, אני מצמיד לכל ענף סיכוי 0.5 (50%). כעת יש 50% שהחתיכה כשרה ו-50% שלא. בגלל דיני ספיקות בדאורייתא עליי להחמיר ובדרבנן ניתן להקל.
תזכורת חשובה: ספק פוזיטיבי ונגטיבי
בטור הקודם עמדתי על כך שיכולים להיות שני מצבים שונים של ספק: ספק פוזיטיבי וספק נגטיבי. ספק פוזיטיבי הוא ספק שנותן משקל שווה לשתי האפשרויות על בסיס מידע שיש לי לגביהן. למשל במטבע הוגנת יש סיכוי שווה ל’עץ’ ול’פלי’, כי אני יודע שהמטבע הוגנת. אבל יש גם ספק נגטיבי, שזה מצב שבו אני נותן משקל שווה לשתי האפשרויות בגלל היעדר מידע (בורות). לדוגמה, מטבע שאין לי שום מידע על המבנה שלה (האם היא הוגנת או לא, וכיצד לא). גם כאן אם אצטרך להמר אני אתן משקל הסתברותי שווה לשתי האפשרויות (כי אין לי שום דרך להעדיף אחת מהן), ולכן גם כאן אני רואה את המצב כספק שקול. אבל השקילות במצב כזה היא תוצאה של בורות (ולא בגלל מידע). לכן זהו ספק נגטיבי. בספר שב שמעתתא ש”א פי”ח עמד בצורה מפורשת על ההבחנה הזאת (בהסבר הריב”ש).
אזכיר שבטור הקודם עמדתי על מצב דומה ביחס לדיני רוב. גם שם ישנם מצבים שיש לי מדד מספרי לרוב (80%, 55%, 99% וכדומה), ואז בדרך כלל זהו רוב פוזיטיבי (שמבוסס על מידע). אבל ברוב המקרים אין לי מדד מספרי כזה. אני יכול לכל היותר לומר שמדובר ברוב גדול או קטן (בטור הקודם הגדרתי שלושה סוגי רוב: מוחץ, מוחלט ורגיל). זהו רוב נגטיבי, שכן הוא אינו מבוסס על מידע ברור. יש לי מידע כללי שרוב הסיכויים הם לאחת משתי האפשרויות, אבל לא מעבר לזה.
מהו ספק ספיקא
מה קורה אם יש לי ספק מאיזו בהמה נלקחה חתיכת הבשר הזאת? אם מחזיר – אז היא לא כשרה גם אם זה שומן, ואם מפרה – אז היא כשרה אם זה שומן אבל אם זה חלב אז לא. זהו מצב של ספק ספיקא, ועץ האפשרויות שמתאר אותו הוא הבא:
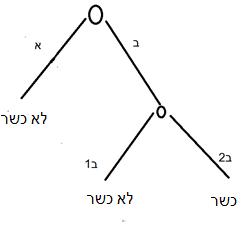
שרטוט ג: ספק ספיקא לחומרא
העיגול העליון הוא המצב העובדתי שבפניי, או השאלה: מהי חתיכת הבשר שבפניי, חלב (א) או שומן (ב)? העיגול השני ממוקם מתחת לענף של שומן (ב), שאז עולה השאלה השנייה (עוד צומת שגם היא מייצגת מצב עובדתי מסופק): האם זהו שומן פרה (ב2) או שומן חזיר (ב1)? כאמור, אם יש לי מידע מלא, עליי ללכת לאורך עץ האפשרויות עם המידע שלי. למשל, אם אני יודע שזהו שומן חזיר, אזי המסלול הוא ימינה בצומת העליונה ושמאלה בתחתונה. בקצה המסלול יש את התוצאה הברורה של מצב כזה: לא כשר. הוא הדין לשומן פרה (ימינה, ימינה: כשר). חלב (שמאלה. וכאן לא משנה אם זה חזיר או פרה, והתוצאה היא לא כשר).
מה קורה אם אינני יודע את התשובה? שוב עליי לעשות חשבון הסתברותי. יש שלושה קצוות לעץ שלנו, אבל לא לכולם יש אותה הסתברות. כל צומת שעברתי על המסלול מייצגת ספק שקול (נגטיבי או פוזיטיבי).[1] לכן כשאני מתקדם לאורך המסלול כל מעבר בצומת מכפיל את התוצאה ב-1/2. למשל, מסלול שעובר את שתי הצמתים (מה שמסתיים ב-ב1 או ב2) הסתברותו 1/2X1/2=1/4. לעומת זאת, מסלול שעובר רק צומת אחת (א) הסתברותו 1/2. אם כן, יש סיכוי 1/4 שזה שומן פרה וסיכוי 1/4 שזה שומן חזיר וסיכוי 1/2 שזה חלב (לא משנה אם חזיר או פרה). לכן במצב כזה יש סיכוי 3/4 שזה לא כשר ו-1/4 שכן. זהו ספק ספיקא לחומרא (רוב הסיכויים הם לחומרא ויש להחמיר).
חשוב להבין שזו רק דוגמה להמחשת הלוגיקה. בדרך כלל ספק ספיקא הוא מצב שמתואר בעץ כזה אבל לקולא, כלומר גרף שבתחתיתו שלוש תוצאות של ‘כשר’ ואחת של ‘לא כשר’ (שם הסיכוי הוא 3/4 להיתר ו-1/4 לאיסור). בהמשך נעסוק בדוגמה כזאת ממסכת כתובות. הסיבה לכך שספק ספיקא הוא בדרך כלל להיתר היא שאם מדובר בספק ספיקא לחומרא כמו אצלנו אין לזה השלכות, שהרי גם בספק אחד יש ללכת לחומרא, אז ודאי שכשרוב הסיכויים הם לכיוון המחמיר יש להחמיר.
ניתן היה לצייר את אותו עץ אפשרויות שמופיע בשרטוט ג בדרך שונה, מלאה יותר:
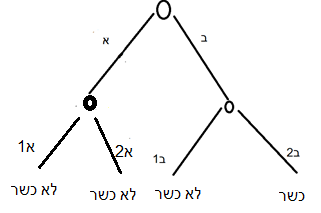
שרטוט ד: ספק ספיקא הצגה מלאה
כאן הצגתי את הספק האם מדובר בחזיר או בפרה גם מתחת לאפשרות שזה חלב (א2 – פרה, א1 – חזיר), למרות ששם זה לא משנה הלכתית. היתרון של הצגה כזאת הוא שכעת לכל תוצאה יש את אותו סיכוי (כי בדרך אליה עברנו שני צמתים). במצב כזה לא צריך לעשות חשבון ומכפלות, וניתן פשוט לספור קצוות ולהגיע ישר לתוצאה: יש שלוש תוצאות של ‘לא כשר’ ואחת של ‘כשר’, ולכן הסיכוי הוא 3/4 לחומרא ולכן יש להחמיר.
שימו לב שאם ההתפלגות של התוצאות הייתה 2-2, כמו בציור הבא, זה לא היה ספק ספיקא:
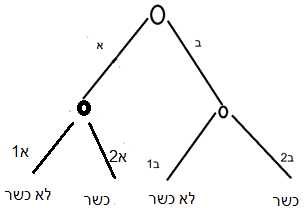
שרטוט ה: עץ דמוי ספק ספיקא שאין בו מכפלה אלא מקבילות
לדוגמה, יש לי ספק אם זו עז או פרה, אבל בשתיהן יש ספק האם זה חלב (שאסור) או שומן (שמותר). לכן כאן הסיכוי לכך שזה לא כשר הוא 1/2, וזהו מצב של ספק אחד ולא ספק ספיקא. זה מקביל לגמרי למקרה של ‘תרי רובי’ שאינו ‘רובא דרובא’ מהטור הקודם. הסברתי שם שכאן אין מכפלה ולכן זה בעצם מצב של רוב בודד. גם כאן אין מכפלה ולכן העץ הזה מתאר מצב של ספק בודד ולא של ספק ספיקא.
ספק ספיקא ורוב: רוב ‘צדדים’
המפרשים דנים בשאלה מדוע אנחנו מרשים לעצמנו להקל במקרה של ספק ספיקא אפילו באיסורי דאורייתא (ראו סקירה למשל כאן). שיטת הרמב”ם היא שספק דאורייתא לחומרא הוא עצמו דין דרבנן. לשיטתו אפשר היה לומר שספק ספיקא הוא ספק דרבנן ולכן מקילים בו. אבל לשיטת רוב הראשונים שהכלל ספק דאורייתא לחומרא הוא עצמו מדאורייתא, ההסבר המתבקש ביותר להקלה בספק ספיקא הוא שמדובר בדין של הליכה אחר הרוב. כאשר יש לנו עץ של ספק ספיקא לקולא (3 אפשרויות ‘כשר’), אזי רוב הסיכויים (0.75) הם שזה כשר, והולכים אחר הרוב. כך באמת מבין הרשב”א (תורת הבית בית ד, שער א). השאלה שעולה כאן היא מדוע מפרשים אחרים לא מקבלים זאת. לכאורה יש כאן רוב ודין הליכה אחר הרוב יכול להסביר הכל. אפשר היה לשאול זאת חזק יותר: למה בכלל צריך את המושג ספק ספיקא, אם יש לנו כבר את דין רוב? חשבו על מצב שהיה כאן ספק פוזיטיבי, כלומר יש לנו מידע שכל ספק כזה הוא באמת 50%. במקרה כזה, בספק ספיקא יש רוב סיכויים ברור להיתר (75%), ואז לא היינו נזקקים בכלל לדין ספק ספיקא. היה כאן דין הליכה אחר הרוב.
המסקנה שעולה מכאן היא שדין ספק ספיקא רלוונטי אך ורק בספקות נגטיביים. כשהספיקות הם פוזיטיביים יש רק את דין רוב. בספיקות נגטיביים יש חידוש מיוחד של התורה שלמרות שאין כאן רוב סיכויים ניתן לראות זאת כרוב. ואכן ראינו בטור הקודם שברוב מצבי הספק (והרוב) מדובר בספק נגטיבי. במצב כזה איננו יודעים מה הסיכוי לכל אחת משתי האפשרויות, ומתוך הבורות הזאת אנחנו מניחים שקילות ביניהן. בספק כזה אין שום הכרח לומר שבאמת יש רוב סיכויים לטובת ההיתר, ולכן אנחנו נזקקים לדיני ספק ספיקא בנוסף לדיני רוב. בספק ספיקא יש צד אחד מול שלושה אחרים, ואין לנו מידע מה הסיכוי האמתי של כל אפשרות (צד), שכן יכול להיות שלצד הבודד יש סיכוי ששקול לשלושת האחרים או אף גבוה מהם. אבל מכיוון שאיננו יודעים את הסיכוי של כל צד, ההלכה אומרת שעלינו להניח משקל שווה לכל אחד מהם.
בספק רגיל אנחנו מניחים שקילות, ואלו דיני ספיקות. כאילו יש כאן ספק שקול של 50% לכל צד. ובספק ספיקא, שכאמור קיים רק בספיקות נגטיביים, אנחנו שוב סופרים צדדים. כאן יש שלושה צדדים לטובת ההיתר, ולכן אנחנו מתירים. כלומר באמת הולכים כאן אחר הרוב, אבל זה לא מדין הליכה אחר הרוב כי אין כאן רוב סיכויים. אלא זהו חידוש של התורה שכשאין מידע הולכים אחרי רוב צדדים: בספק רגיל זה צד אחד מול אחד, ובספק ספיקא זה צד אחד מול שלושה ולכן מתירים.
מושג ה’צדדים’ הוא הלכתי ולא הסתברותי
חשוב מאד להבין את ההיגיון (או חוסר ההיגיון) שבבסיס התמונה הזאת. לשם כך עלינו לחזור לדוגמה של חלב ושומן בחזיר ופרה. העובדה שבספק רגיל בין פרה לחזיר אנחנו מניחים שיש 50% שזו פרה ו-50% שזה חזיר זה סתם דין. אין לנו שום אינדיקציה לכך שהספק הוא שקול, אבל בהיעדר מידע אחר זוהי ההנחה שלנו. זהו ספק נגטיבי. כעת נוסף לנו עוד ספק אם זה חלב או שומן, וגם הוא כמובן ספק נגטיבי. כעת הגענו למצב של ספק ספיקא (כי אין לנו מידע על ההתפלגות בין פרה לחזיר ובין חלב לשומן), וכפי שראינו סופרים צדדים והולכים אחרי רוב הצדדים (שזה אינו הדין הרגיל של הליכה אחר הרוב).
אבל במצב כזה אין הכרח לדבר על ארבעה צדדים. הבחירה לפצל ספק ספיקא ולראות כאן ארבעה צדדים היא שרירותית במידת מה. בה במידה יכולנו גם לומר שיש כאן רק שני צדדי ספק: כשר או לא כשר, וזה עצמו ספק עם שני צדדים, ולכאורה בהיעדר מידע עלינו לתת סיכוי שווה לשניהם ולכן יש כאן ספק לחומרא. כך גם יכולנו לומר שיש כאן שלושה צדדים (כמו בשרטוט ג) ואז יש כאן רוב של 2/3 ולא של 3/4. ההנחה שענף א הוא בעל משקל כפול משני האחרים מבוססת על הסתכלות הסתברותית שאין לה בסיס אמתי (מדובר בספק נגטיבי). זוהי הסיבה לכך שהצעתי את ההצגה המלאה בשרטוט ד. שם יש בספק ספיקא ארבעה צדדים, ואז ההליכה אחר הרוב להיתר נראית טבעית יותר בלי להיזקק להנחות הסתברותיות על משקלים שונים של הקצוות. לכל המסלולים, או הקצוות שלהם, יש אותו משקל.
אבל יש עוד אפשרויות להגדרת צדדים. לא רק שנים או שלושה כמו שראינו כעת, אלא בה במידה ניתן לפצל את עץ האפשרויות ליותר צדדים (שבעה, עשרה, מאה). לדוגמה, יכולנו לדון האם זה חזיר יבלות, חזיר רגיל, או ג’ירפה? ובצד הכשר לדון האם זו פרה הולנדית או אוסטרלית, או אולי עז. אפשר לדון האם זה החלק הרך של החלב או החלק הקשה וכן הלאה. אם לכל צד כזה אנחנו נותנים משקל שווה (בהיעדר מידע) אנחנו יכולים להגיע לכל תוצאה הלכתית שתרצו. שימו לב שאין כאן שום דבר לא הגיוני מבחינה סטטיסטית. זה לא פחות הגיוני מהבחירה להציג ספק ספיקא כעץ של ארבעה צדדים.
המסקנה היא שהחלוקה של ספק ספיקא נגטיבי לארבעה צדדים היא החלטה שרירותית, ואין לה בסיס עובדתי או סטטיסטי. בספיקות פוזיטיביים יש לחלוקה כזאת בסיס הסתברותי, אבל כפי שראינו בספק פוזיטיבי אין צורך להגיע לדיני ספק ספיקא, שכן שם יש לנו את דין רוב הרגיל שהולכים אחריו. בספק ספיקא מדובר תמיד בספק נגטיבי. זה אמנם נראה לכאורה כמו חשבון הסתברותי, אבל זה מבוסס על תשתית לא הסתברותית. חלוקת הצדדים בבעיה הנתונה היא דין, כלומר שיקול הלכתי, והיא שעומדת בבסיס החישוב ההסתברותי. אחרי שיש לנו צדדים אנחנו מעניקים להם משקל שווה ואז סופרים אותם כאילו מדובר בהסתברויות. המסקנה היא שהחלוקה לצדדים היא היא מוקד הדיון בהלכות ספק ספיקא, וזו שאלה הלכתית ולא הסתברותית. אבל מכאן והלאה מבחינתנו זהו חישוב הסתברותי (בדומה למה שראינו בטור הקודם לגבי רוב ו’תרי רובי’ בעגונות).
זה מביא אותנו לשני כללים בהלכות ספק ספיקא שקשורים לתמונה שתיארתי עד כאן.
שם ספק חד הוא
הגמרא בכתובות ט ע”א דנה בטענת “פתח פתוח מצאתי” של הבעל לגבי אשתו:
אמר רבי אלעזר: האומר פתח פתוח מצאתי נאמן לאוסרה עליו.
הבעל טוען שהיא לא בתולה, ואם נבעלה תחתיו היא נאסרת עליו ועל הבועל. ר”א אומר שהבעל נאמן והיא נאסרת עליו. הגמרא מקשה:
ואמאי? ספק ספיקא הוא! ספק תחתיו ספק אין תחתיו, ואם תמצי לומר תחתיו – ספק באונס ספק ברצון.
מבואר בקושיית הגמרא שבטענת “פתח פתוח” יש מצב של ספק ספיקא: ספק אם זה קרה תחתיו או לא (אם לא נבעלה תחתיו היא אינה נאסרת), וגם אם כן – ספק באונס ספק ברצון (רק אם נבעלה תחתיו ברצון היא נאסרת). אם כן, לכאורה הבעל אינו יכול להיות נאמן לאוסרה שהרי בספק ספיקא הולכים לקולא ופוסקים שהיא מותרת. קשה על ר”א.
הגמרא מיישבת בשתי צורות:
לא צריכא – באשת כהן. ואיבעית אימא: באשת ישראל, וכגון דקביל בה אביה קידושין פחותה מבת שלוש שנים ויום אחד.
אם מדובר באשת כהן אין הבדל בין אונס לרצון (בשני המקרים היא נאסרת עליו) ולכן זה רק ספק אחד. תירוץ שני הוא שאביה קיבל את קידושיה כשהייתה פחות מבת שלוש שנים, ובמצב כזה לא ייתכן שנבעלה לפני הקידושין כי בתוליה היו חוזרים.
בתוד”ה ‘ואי בעית אימא’, שם, מקשים:
א”ת אכתי איכא ספק ספיקא – ספק באונס ספק ברצון, ואת”ל ברצון – ספק כשהיא קטנה ופתוי קטנה אונס הוא וכו’.
תוס’ מקשה על האוקימתא השנייה (שאביה קידשה בת פחות משלוש ויום), שעדיין יש כאן ספק ספיקא: ספק באונס או ברצון, וגם אם ברצון יש אפשרות שזה היה בעודה קטנה ועדיין זה נחשב כאונס (פיתוי קטנה נחשב כאונס כי אין לה דעת).[2]
העץ שבו מדובר דומה לעץ בשרטוט ג או ד (שהוא הצגה מלאה של אותו ספק ספיקא כמו ג), אבל הפעם לקולא (יש שלוש אפשרויות של היתר):
במקרה שלנו הספק הראשון הוא ספק אונס (א) ספק רצון (ב), ואם זה היה ברצון יש עוד ספק אם היא הייתה קטנה (ב1) או גדולה (ב2). אם נשתמש בהצגה המלאה של שרטוט ד (שבה הספק השני מופיע גם תחת אפשרות א), אנחנו מקבלים ארבע אפשרויות בקצוות: אונס קטנה (א1), אונס גדולה (א2), רצון קטנה (ב1) ורצון גדולה (ב2). מתוכן בשלוש היא מותרת ובאחת היא אסורה.
תוס’ עונה:
וי”ל דשם אונס חד הוא.
האפשרות שזה היה ברצון כשהיא קטנה (ב1) והאפשרות שזה היה באונס בגדולה או קטנה (א1 ו-א2) הן אותה אפשרות. כל אלו הן אפשרויות אונס, ושם אונס חד. לכן בעצם יש לנו רק ספק אחד, כמו בשרטוט ב מלמעלה (אפשרות א מייצגת את שלוש אפשרויות האונס), אונס או רצון:

לכן עלינו לאסור אותה כדין ספק רגיל.
המפרשים לוקחים את העיקרון של תוס’ והופכים אותו ליסוד כללי בדיני ספק ספיקא: כאשר שם ספק חד אנחנו רואים את כל האפשרויות הללו כאפשרות אחת. זה מבוסס כמובן על מה שראינו למעלה, שהחלוקה לאפשרויות (צדדים) היא עניין הלכתי ולא הסתברותי. השיקול ההלכתי של תוס’ הוא שכל האפשרויות שמובילות לאונס צריכות להיחשב כאפשרות אחת.
אבל אם רואים את כל אפשרויות ההיתר כאפשרות אחת, אין בעולם ספק ספיקא? לכאורה כל ספק ספיקא אנחנו יכולים להפוך כך לספק אחד. למשל, הספק ספיקא של תחילת הסוגיה: ספק באונס ספק ברצון ספק תחתיו ספק לא, אפשר לומר ששלושת אפשרויות ההיתר (אונס תחתיו ולא תחתיו ורצון לא תחתיו) שמן אחד: כולן היתר. שם היתר חד. אך זוהי טעות. הכלל של תוס’ עוסק בהנמקה ולא בדין. כשההנמקות הן מאותו סוג (=אונס) זה נחשב שם ספק חד. אבל כשהדין הוא משותף (=מותרת) זה לא מתאחד לצד אחד. כשמדברים על אונס זו הנמקה לכך שהאישה לא נאסרת, וסוגי אונס שונים הם אותו נימוק: אונס.
זה דומה למה שראינו למעלה שלא מחלקים את הספק לצדדים נוספים באופן מלאכותי (אולי חזיר ואולי חזיר יבלות). אם היינו מפרידים בין פיתוי ואונס קטנה לבין אונס גדולה יכולנו באותה מידה לפרק את אפשרויות האונס לעוד כמה אפשרויות שונות: אונס על ידי החזקת הידיים, עם או בלי קשירה, הטעיה וכדומה. כל אלו הם סוגי אונס ואין טעם לעשות מזה צדדים שונים: שם אונס חד. כאשר מדברים על שם היתר חד, זהו איחוד בין הנמקות שונות רק בגלל שהן מובילות לאותו דין. איחוד כזה לא עושים. הבסיס לעיקרון הזה הוא שהספק שלנו עוסק בהנמקות ובעובדות (בעיגול ובענפים שיוצאים ממנו) ולא בדין (שהוא רק תוצאה של האפשרויות הללו). לכן הכלל של ‘שם ספק חד’ עוסק במצב שבו מה שכתוב בצד הענפים הרלוונטיים (ההנמקות) הוא מאותו שם. אבל במקרה שהנורמות שכתובות בקצה של כמה מהמסלולים דומות (כולם ‘מותרת’ או כולם ‘כשר’ וכדומה) – את זה כמובן לא מאחדים. אם היינו מאחדים את זה לא היה קיים בעולם ספק ספיקא.
מהתמונה הזאת תוכלו להבין שהעיקרון של תוס’, ‘שם ספק חד’, הוא פועל יוצא מהתיאור שנתתי למעלה (בצורה דומה עמד על כך הרב ז”נ גולדברג במאמרו כאן). כמובן שאם מדובר בספיקות פוזיטיביים כל הדיון הזה אינו רלוונטי. ראשית, ראינו שבספיקות כאלה בכלל לא נכנסים לשאלות של ספק ספיקא. הדין נקבע סטטיסטית. שנית, בספיקות כאלה יש חלוקה טבעית של הצדדים ולא צריך להתלבט לפי שמותיהם: צד בספק פוזיטיבי הוא מה שסיכוייו הם 50%. אם יש סכום של כמה צדדים שנותנים יחד 50% הם יאוחדו בלי קשר לשמם. אם נניח אני יודע שהסיכוי לכך שהאישה פותתה כקטנה או נאנסה הוא 50% והסיכוי שהוא עשתה זאת לרצונה כגדולה הוא 50%, אזי אני בספק שקול, ולא אכפת לי שהצד הראשון הוא צירוף של כמה צדדים. אני בספק שקול כי באמת יש 50% שהיא מותרת ו-50% שהיא אסורה. זהו שיקול סטטיסטי ולא הלכתי. אבל כאמור לענייננו רלוונטיים רק ספיקות נגטיביים, ושם אנחנו נזקקים לכללי ספק ספיקא ושמות הספק הם שקובעים את הצדדים הרלוונטיים.
ספק ספיקא מתהפך
כמה ראשונים ואחרונים כתבו שבכללי ספק ספיקא יש עיקרון נוסף, שספק ספיקא צריך להיות ‘מתהפך’. לשיטתם, ספק ספיקא שאינו מתהפך אינו ספק ספיקא. עליי להעיר שהכלל הזה אינו מוסכם על כל הפוסקים (הש”ך מאמץ אותו בחום, אבל מהרי”ט ופר”ח חולקים עליו), אבל הוא מקובל אצל רבים. כאן נבחן אותו לפי השיטות שהוא קיים.
מקור אחד לדברים הוא בתוס’ ישנים כתובות ט ע”ב. נקדים שאישה שנישאה לא בתולה כתובתה מנה (ולא מאתיים). לכן בטענת “פתח פתוח” של הבעל יש דיון גם באיסור שלה על בעלה וגם בממון (גובה החיוב בכתובה). בתוד”ה ‘אי למיתב’, שם, דייק מהגמרא שלעניין ממון הבעל היה נאמן להפסידה כתובה. ומיד הוא מקשה מדוע הבעל נאמן להפסידה ממון הרי זה ספק ספיקא: ספק אם הוא בקיא בפתח פתוח (יודע לאבחן שאשתו אינה בתולה), וגם אם כן, ספק באונס ספק ברצון. בעצם יש ספק האם היא בכלל בעולה (כי אולי הוא לא יודע לאבחן ובעצם היא בתולה), ואם בעולה יש ספק האם באונס או ברצון. תוס’ והמפרשים שם מיישבים זאת בדרכים שונות.
אבל בתו”י שם יישבו זאת כך:
וי”מ דהכא לא חשיב ספק ספיקא דאין יכולין להתהפך ולומר ברישא ספק באונס ספק ברצון ואת”ל ברצון ספק וכו’. ולהכי לא חשיב אלא חדא ספיקא.
הוא טוען שספק ספיקא חייב להיות כזה שניתן להחליף בין הצמתים בשרטוטים ג וד’. למשל, בדוגמה שלמעלה ניתן להסתפק האם תחתיו או לא, ואז להסתפק גם אם זה תחתיו – האם באונס או ברצון. ואפשר להחליף את הצמתים ולהסתפק האם באונס או ברצון, ולאחר מכן גם אם ברצון – ספק האם תחתיו או לא. רק כאשר אפשר להחליף את הצמתים זה בזה מדובר בספק ספיקא. אם הצמתים לא ניתנים להחלפה זה נחשב כספק אחד ואין להקל בו. במקרה של תו”י זהו ספק ספיקא שאינו מתהפך, שכן אי אפשר להסתפק האם באונס או ברצון, ואז להסתפק האם הוא בקיא בפתח פתוח. הסיבה לזה היא שאם הוא לא בקיא בפתח פתוח אז היא בכלל בתולה וממילא אין מה להסתפק כיצד נבעלה (באונס או ברצון). היא לא נבעלה. כאמור, המפרשים והפוסקים הרחיבו את הכלל להיות עיקרון כללי בהלכות ספק ספיקא.
ההסבר ההגיוני לכלל הזה אינו ברור. הרמ”ע מפאנו מציע שמכיוון שניתן להעלות את צדדי הספק רק בסדר אחד ולא בשני, אזי יש לנו ספק בזה גופא, האם להסתפק בסדר האחד ואז הולכים לקולא או בסדר השני ואז עלינו להחמיר. ומכיוון שזה גופו ספיקא דאורייתא עלינו להחמיר בו. אבל הסבר זה אינו הגיוני משתי סיבות לפחות:
- הרי זה גופו יוצר ספק ספיקא: האם להסתפק בסדר כזה או בסדר השני, ואם מסתפקים בסדר הראשון עדיין יש שם את הספק היחיד שנותר. אז למה שלא נקל בספק ספיקא כזה? ניתן לתהות בדומה לזה על שיטות הראשונים שסוברים שספק דאורייתא לחומרא מדאורייתא: למה לא נחמיר גם בספק ספיקא, שהרי זהו גופו ספק דאורייתא (ספק שמא יש לנו מקרה של ספק דאורייתא לחומרא). האחרונים כבר דנו בזה (ראו למשל בשערי ישר שער א פ”ג ופי”ט). ניתן לבאר זאת בכך שאם יש לנו ספק האם להסתפק אין עלינו חובה להסתפק. את זה דין ספיקא דאורייתא לחומרא לא מטיל עלינו.
- די לנו בכך שיש סדר אחד של ספיקות שיוצר ספק כפול כדי להקל. מה אכפת לי שיש סדר אחר שבו הדין יוצא לחומרא?! זה כמו שבקל וחומר די לי שיש ניסוח אחד כדי להוכיח את הדין, גם אם פרכנו את הניסוח ה’מאונך’ (ראו בטור 537).
אנו נשוב להסבר הכלל הזה אחרי שנדון ביחס בין שני הכללים.
היחס בין שני הכללים: התהפכות ושם ספק חד
הפוסקים מביאים דוגמה נוספת לספק ספיקא שאינו מתהפך, לגבי פגימה בסכין שחיטה (ראו ש”ך בכללי ספק ספיקא אות יג בשם האגור). מהגמרא בחולין י ע”ב עולה שמי ששחט בהמה ומצא לאחר השחיטה שהסכין פגומה – השחיטה פסולה והבהמה נחשבת נבלה. יש ראשונים שהקשו מדוע לא נתיר את הבהמה מספק ספיקא: ספק אם הסכין נפגמה במהלך השחיטה או אחריה (כאשר הסכין פגעה במפרקת), וגם אם הסכין נפגמה במהלך השחיטה – אולי זה קרה לאחר שרוב הצוואר כבר נחתך (ואז השחיטה לא נפסלת). התשובה היא שזהו ספק ספיקא שאינו מתהפך, כיוון שאם נתחיל בספק השני – האם הסכין נפגמה קודם שחיטת רוב הצוואר, לא נוכל כמובן להמשיך ולומר שגם אם נפגמה קודם שחיטת רוב הצוואר, אולי נפגמה לאחר השחיטה.
בדוגמה הזאת תוכלו לראות שניתן גם לטעון שזה שם ספק חד. בין אם נפגמה אחרי השחיטה או אחרי רוב השחיטה שם ספק חד הוא: נפגמה אחרי רוב השחיטה הבהמה אינה נבלה. הרי בה במידה אפשר היה להוסיף עוד המוני צדדים: אולי נפגמה אחרי 51% מהשחיטה, אחרי 54%, אחרי 80% אחרי 98% ולגמרי אחרי השחיטה. כל אלו הם אותו צד עצמו: שהסכין נפגמה בשלב שבו השחיטה כבר כשרה.
זהו רמז ראשוני לתהייה של כמה לומדים מדוע בכלל לראות את שני הכללים הללו ככללים שונים: על פניו נראה ששם ספק חד וספק ספיקא שאינו מתהפך זה אותו כלל עצמו. כדי לחזק את זה, ראו כאן שרעק”א הבין את תירוץ התוס’ בכתובות ט ע”א שדיברו על שם אונס חד, שבעצם כוונתם לומר שזהו ספק ספיקא שאינו מתהפך. אם נתחיל מהספק שמא נבעלה באונס או ברצון, לא נוכל להמשיך ולומר, את”ל ברצון אולי נבעלה בקטנותה. שהרי בקטנותה הבעילה אינה נחשבת ברצון שכן פיתוי קטנה אונס הוא.
משתי הדוגמאות הללו ניתן היה להסיק ששני הכללים הללו זהים. ובאמת ישנה נטייה אצל רבים לראות אותם כשתי פנים של אותו כלל עצמו. אם אכן זהו המצב, אין שאלה מדוע ספק ספיקא צריך להיות מתהפך. ההסבר לזה הוא כמו ההסבר לכלל שם ספק חד שראינו למעלה, כלומר ההתהפכות נדרשת כדי שבאמת יהיו לנו צדדי ספק שונים שיוצרים רוב צדדים לקולא (כך, למשל, טוען הרב שלמה לוי בתחילת מאמרו. לאחר מכן הוא דוחה זאת). אלא שכפי שנראה כעת זה כנראה לא נכון.
אבל כבר בדוגמה של תוס’ בכתובות ניתן לראות ששני הכללים אינם זהים. לא כמו שהניח רעק”א, בהחלט ניתן להסתפק על הצד שנבעלה ברצון שמא נבעלה קטנה. נכון שלדינא בעילת קטנה ברצון נחשבת כאונס ולכן בקצה המסלול כאן יהיה רשום בשני הצדדים ‘מותרת’ (ראו למשל למעלה בשרטוט ד, שמתחת לענף א יש התפצלות של ספק שבשני צדדיו יש אותו דין). לכל היותר ניתן לטעון שאין טעם להסתפק כי שם ספק חד (שהרי זה וזה מקרי אונס).[3] כלומר הדוגמה של תוס’ כתובות היא דוגמה לספק ספיקא כן מתהפך אלא ששם אונס חד (כל הנימוקים להיתר הם אותו נימוק: אונס) ולכן מחמירים. זה לא דומה למקרה של השחיטה ששם בכלל אי אפשר להסתפק בסדר הפוך, כלומר שזה גם לא מתהפך וגם שם ספק חד. אעיר כאן שגם בשאלה שהזכרתי בתחילת הטור מובאת דוגמה של הש”ך לספק ספיקא לא מתהפך בשחיטה, וגם שם הוא טוען שזה לא מתהפך כי אין נפ”מ לספק השני על הצד של הספק הראשון. אבל כפי שטענתי כאן, זה שאין נפ”מ לא אומר שהספק ספיקא אינו מתהפך. כדי שמבנה כזה ייחשב לא מתהפך צריך שבכלל אי אפשר יהיה להסתפק את הספק השני (כמו שראינו במקרה של תו”י בכתובות).
עד כאן ראינו שייתכן מצב שבו שם ספק חד אבל הספק מתהפך (זה המקרה של תוס’ כתובות). האם ייתכן מצב שבו הספק אינו מתהפך אבל שם הספק אינו חד? השחיטה אינה מקרה כזה, כי ראינו ששם זה גם לא מתהפך וגם שם ספק חד (הספק הוא האם נפגם אחרי שהשחיטה כבר כשרה). אבל המקרה של תו”י בכתובות ט ע”ב שהוא המקרה הראשון שראינו של ספק ספיקא לא מתהפך, ושם נראה ששם הספק אינו חד. אם הבעל לא יודע לאבחן בתולים – כי אז ההיתר הוא מכוח זה שבכלל לא נבעלה. אבל אם הוא יודע לאבחן אלא שנבעלה באונס – כי אז ההיתר הוא מנימוק שונה: שנבעלה באונס. אלו שני שמות שונים של צדדי היתר שמובילים לאותה נורמה. ראינו למעלה ששם ספק חד נאמר על הנימוק (הצדדים) ולא על הנורמה עצמה.
ממה שראינו כאן עולה בבירור ששני הכללים הללו אינם זהים, ובעצם כפי שראינו הם בלתי תלויים: יש ספק ספיקא שנחמיר בו כי אינו מתהפך למרות ששמות הצדדים להיתר אינם חד (תו”י בכתובות ט ע”ב), ויש ספק ספיקא שנחמיר בו כי שמות הצדדים חד למרות שהוא מתהפך (תוס’ כתובות ט ע”א). כך עולה גם מעצם העובדה שיש שיטות שלא דורשות התהפכות של ספק ספיקא, אבל כן מקבלות את הכלל שאם שם ספק חד זה אינו ספק ספיקא.[4]
אזכיר כעת שהכלל שם ספק חד הוא הגיוני ומתבקש כפי שהוסבר למעלה. אלא שאם אכן אנחנו צודקים בכך ששני הכללים הללו הם בלתי תלויים, עלינו לשוב ולחפש הסבר נפרד לכלל שמחייב התהפכות. עד עתה טרם מצאנו לו הסבר מספק.
הסבר הכלל של ספק ספיקא מתהפך
ראינו בטור הקודם ובטור הנוכחי שבניגוד למה שנוהגים לחשוב כללי הספק והרוב יסודם בהסתכלות הסתברותית. כללי ספק ספיקא נחוצים רק במצב שבו מדובר בספק נגטיבי (ואלו הרוב המוחלט של המצבים והדוגמאות בהלכה). במצבים כאלה אין לנו באמת מספרים שמתארים את ההסתברות, וההחלטה שספק כזה הוא שקול היא החלטה הלכתית ולא הסתברותית. אבל מכאן והלאה מבחינתנו יש לנו שאלת הסתברותית שמתוארת על ידי עץ שבו כל צומת היא ספק שקול (נגטיבית), ועלינו להכריע אותה במשקפיים הסתברותיים. הסיכוי של כל תוצאה הוא מכפלת הסיכויים של הצמתים שעברנו בדרך. אם כן, עלינו לבחון עץ של ספק ספיקא ולשאול את עצמנו מה משמעות העובדה שהוא לא מתהפך. אני יכול להציע לכך שני הסברים, ואתאר אותם כעת.
הסבר ראשון: בין ספירת צדדים להסתברות
ההסבר הראשון הולך בדרכו של הרמ”ע מפאנו שהוזכרה למעלה, אבל במסגרת מושגית מעט שונה. נקודת המוצא שלנו היא שמדובר בספיקות נגטיביים. אם כך, אנחנו בעצם סופרים צדדים ולא סיכויים. הכלל היסודי שעומד בבסיס ההיתר של ספק ספיקא הוא שרוב צדדים גם הוא רוב, למרות שהוא לא מצביע בהכרח על רוב הסתברותי. במצב של ספק רגיל יש צד אחד לכל כיוון, ולמרות שאין לנו דרך לבחון האם יש כאן 50% לכל אחד מהם ההלכה אומרת לנו להתייחס לזה כספק שקול ולהחמיר (בדאורייתא). בספק ספיקא יש לנו שלושה צדדים להיתר מול אחד לאיסור, ולכן הולכים אחרי רוב הצדדים ומקילים. מה קורה בספק ספיקא שאינו מתהפך?
הרמ”ע מפאנו הציע שבמצב כזה אנחנו בספק האם להציג את סדר הספיקות באופן שנוצר ספק ספיקא (ואז אפשר להקל), או באופן ההפוך שבו זהו ספק בודד (ואז יש ללכת לחומרא). הוא טען שהספק הזה עצמו הוא ספק דאורייתא ויש להחמיר בו. אבל למעלה ראינו שזהו הסבר בעייתי. כאן אציע וריאציה קטנה על ההסבר שלו. נתייחס למצב הזה כספק האם לצייר עץ אפשרויות של ספק ספיקא (כלומר שלושה צדדים להיתר ואחד לאיסור) או של ספק רגיל (ואז יש צד להקל וצד לאסור), שלצורך ההשוואה נציג אותו כשני צדדים להיתר ושניים לאיסור (זוהי הצגה מפורטת יותר של המצב – בדומה למה שראינו בשרטוט ד למעלה).
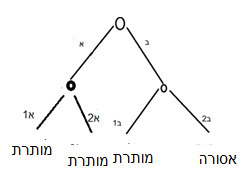
כדי להדגים את הניתוח, ניטול את הדוגמה של ספק ספיקא לא מתהפך שאין בו שם ספק חד (זה המקרה שאותו עלינו להסביר), כלומר את המקרה של תו”י בכתובות ט ע”ב: ספק אם הוא בקיא בפתח פתוח או לא, וגם אם הוא בקיא – ספק האם באונס או ברצון. בסיטואציה כזאת יש לנו שתי אפשרויות לשרטט את המבנה הזה. האפשרות הראשונה היא להציג אותו לפי סדר הספיקות שתיארתי כאן, ואז נקבל את העץ הבא:
כאשר א מייצג את האפשרות שהוא לא בקיא (כלומר הפתח לא היה פתוח), ואז אין שאלה של אונס ורצון והיא מותרת. ב מייצג את האפשרות שהוא בקיא (כלומר הפתח אכן פתוח), ואז זה תלוי האם זה באונס (ב1) או ברצון (ב2). יש כאן שלושה צדדים להיתר ואחד לאיסור.
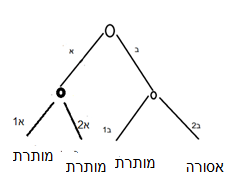
אפשרות שנייה היא להפוך את סדר הספיקות, ולהתחיל בספק האם זה היה באונס או ברצון. ראינו שבמצב כזה לא נוכל להמשיך ולהסתפק אם הוא בקיא או לא (כי הספק הראשון מניח שהפתח אכן היה פתוח). לכן במקרה כזה נקבל עץ של ספק אחד (באונס או ברצון). אנחנו נייצג גם אותו בצורה של עץ כפול אבל הנורמות שבתחתית מחולקות באופן שווה בין צדדי היתר ואיסור:
כאשר א מייצג את האפשרות שזה אונס – ואז בכל מקרה היא מותרת, וב’ מייצג את האפשרויות שזה רצון – ואז בכל מקרה היא אסורה. אין כאן באמת אפשרות שהוא בקיא (1) ולא בקיא (2), ואני מפצל כל ענף לשניים רק כדי שהבסיס להשוואה לעץ הקודם יהיה זהה.
כעת אני מציע בעקבות הרמ”ע מפאנו להתייחס לשני העצים הללו כשתי אפשרויות שקולות, ולכן עלינו לספור את כל הצדדים שכתובים בתחתית שני העצים. יש לנו שמונה אפשרויות שכל אחת בהסתברות 1/8 (ולא ארבע שכל אחת בהסתברות 1/4 כמו בספק ספיקא רגיל). אני מקבל כאן בסך הכל חמש אפשרויות להיתר ושלוש לאיסור. יש כאן רוב אפשרויות להיתר, אבל רוב יותר קטן מאשר בספק ספיקא רגיל. כאן זה 5/8 ושם זה 3/4. כעת עלינו לשוב ולזכור שמדובר כאן בהשוואת צדדים ולא בהשוואת סיכויים, שהרי זהו רוב נגטיבי (אין דרך לכמת את הסיכוי שנבעלה לפני או אחרי, והאם הוא בקיא או לא בקיא). אבל ראינו שרוב צדדים לא בהכרח משקף רוב הסתברותי, ורק ההלכה מורה לנו להתיייחס אליו כאינדיקציה לרוב הסתברותי. הצעתי היא שכדי שנקבל רוב צדדים כרוב הסתברותי ההלכה דורשת רוב מכריע של צדדים, לפחות 3/4 (או 6/8). אם כך, אז רוב צדדים קטן יותר, למשל של 5/8, אינו מספיק, כי יש חשש שאין כאן רוב הסתברותי ולכן באיסור דאורייתא לא סומכים עליו.
זהו הסבר דומה מאד לזה שהצעתי בטור הקודם ל’תרי רובי’. שם הסברתי שמכיוון שמדובר ברוב נגטיבי ואין לנו דרך לבדוק את הסיכוי המספרי, אנחנו דורשים הכפלה כדי לוודא שיש כאן הסתברות של רוב מוחלט. הוא הדין בהצעה שתוארה כאן לספק ספיקא. זהו לכאורה הסבר אפשרי מדוע ספק ספיקא שאינו מתהפך נחשב כספק אחד, כלומר איננו יכולים להקל בו.
אבל במבט נוסף נראה שהניתוח הזה אינו סביר. הסדר ההפוך של הספיקות מתחיל בשאלה האם זה היה באונס או ברצון ומתעלם לגמרי מהאפשרות שהיא כלל לא נבעלה, כלומר שהבעל פשוט טעה כי אינו בקיא. אבל ברור שיש אפשרות כזאת, היא רק לא מופיעה על העץ הזה בגלל מגבלות התיאור. לכן לא סביר להתייחס לעץ הזה כאפשרות שקולה לעץ של הספק ספיקא הרגיל שמציג את כל האפשרויות. העץ שמייצג את המקרה נאמנה הוא רק העץ הרגיל. העץ האחר הוא פיקטיבי ואין טעם להתחשב בו. לכן אין טעם לספור את הקצוות של שני העצים כאילו מדובר בשתי אפשרויות לתאר את המקרה.
המסקנה היא שרק העץ הרגיל מתאר אל נכון את המקרה במצבים אלו. העץ השני אינו אמתי ואין טעם להתחשב בו. אמנם לעץ המדובר במקרה כזה יש תכונה שאינו מתהפך, וכנראה זה הגורם שמונע מאיתנו להשתמש בו לקולא. כעת עלינו לחפש הסבר מדוע זה שהעץ אינו מתהפך מחליש את ההיתר.
הסבר שני: תלות בין אירועים
ההסבר הזה יוצא מנקודת מוצא שלפיה למרות שכל ספק בכל צומת אינו באמת ספק שקול הסתברותית (זו רק הנחה מתודולוגית, שכן מדובר בספק נגטיבי), עדיין מכאן והלאה אנחנו רואים את זה כחישוב הסתברותי. העוקץ לפי הצעתי כאן הוא בדיוק בנקודה הזאת. בחישובים הסתברותיים אם יש חשיבות לסדר ההתרחשות פירוש הדבר הוא שיש תלות סטטיסטית ביניהם.
נניח שאנחנו עוסקים במיתת עריסה של תינוקות (ראו על כך בטור 144). הסיכוי לכך שתינוק A ימות מות עריסה הוא P(A), וזה בערך 1/8,000. מה הסיכוי שימותו שני תינוקות מות עריסה? אם מדובר בשני אירועים בלתי תלויים אזי הסיכוי לכך הוא מכפלת הסיכויים: P(A)*P(B). אבל אם שני התינוקות הם מאותה משפחה אז יש מקום לטענה שיש גורם גנטי כלשהו שמשפיע על תמותת התינוקות, ולכן אם ראינו שתינוק אחד מת, הסיכוי שהתינוק השני ימות הוא כבר גבוה יותר. זהו מצב שבו יש תלות בין שני האירועים (יש גורם שמשפיע על שניהם). במצב כזה הסיכוי לכך שימותו שניהם אינו מכפלת ההסתברויות של כל אחד (זה רק כשאין תלות), אלא: P(B/A)*P(A), כאשר PB/A) הוא הסתברות מותנה. אם יש תלות בין האירועים A ו-B פירוש הדבר שהסיכוי שיקרה B, P(B), שונה מהסיכוי שיקרה B בהנחה שקרה A, כלומר מ-P(A/B). במקרה שלנו ההסתברות המותנה גדולה יותר מההסתברות המוחלטת P(B), ולכן גם המכפלה גדולה יותר. המסקנה היא שאם יש תלות בין שני האירועים זה אומר שההסתברות של השני משתנה (במקרה הקודם – גדלה) אם קרה הראשון.
כעת נשוב לספק ספיקא שאינו מתהפך. כדי שהאישה תיאסר צריכים לקרות שני אירועים: 1. שהאישה לא בתולה (וזה רק אם הבעל בקיא בפתח פתוח (יודע לאבחן בתולים) – והוא אבחן שהיא אכן לא בתולה). 2. הפתח שהבעל אבחן הוא תוצאה של בעילה ברצון ולא באונס. מהו הסיכוי ששני אלו יקרו (שהיא בעולה ושהבעילה היא ברצון)? לכאורה זו מכפלת הסיכויים של כל אחד משני האירועים: P(A)*P(B). אבל זה רק כאשר הספק ספיקא מתהפך, כלומר כשיש אי תלות בין האירועים. אבל אם יש חשיבות לסדר הופעת האירועים, כלומר אירוע B יכול לקרות רק אם קרה קודם אירוע A, משמעות הדבר היא שיש תלות ביניהם. במצב כזה, הסיכוי לכך שהיא אסורה הוא P(B/A)*P(A). אבל כאמור כשיש תלות ההסתברות המותנה יכולה להיות גדולה מההסתברות המוחלטת P(B). היא יכולה גם להיות קטנה יותר (יש גם סוגי תלויות כאלה), אבל יש גם אפשרות שהוא גדול יותר.
המסקנה היא שאם הספק ספיקא לא מתהפך, יש תלות בין האירועים (הצמתים בעץ), ולכן הסיכוי לכך שהאישה אסורה יכול להיות גדול יותר משחשבנו. במצב כזה אין ודאות שהסיכוי לכך שהיא אסורה הוא קטן דיו, ואפילו לא ברור שיש רוב לסיכויים שהיא מותרת. לכן בספק ספיקא כזה לא מתירים את האישה. זהו הסבר הסתברותי אפשרי לכך שספק ספיקא לא מתהפך אינו מתיר את האישה.
שתי סיבות לאי התהפכות של ספק ספיקא: תוכנית וסטטיסטית
כאשר מתבוננים בדוגמה שמלווה אותנו (הספק אם הבעל בקיא ואם נבעלה ברצון), נראה שההסבר הזה לא מחזיק מים. זה שאי אפשר להפוך את צדדי הספק אינו עניין לתלות סטטיסטית אלא לתוכן האירועים המדוברים. בקיצור, לא נראה שהסיכוי לכך שנבעלה ברצון באמת גדול יותר בגלל חוסר ההתהפכות. אם הבעל יודע לאבחן בתולים, זה לא משנה את יחס הסיכויים בין בעילה ברצון לבעילה באונס, אלא רק מאפשר לנו לשאול את השאלה (כי אם לא נבעלה אין טעם לדון האם נבעלה ברצון או באונס). לכן במקרה המסוים הזה לא סביר לומר שחוסר ההתהפכות משנה את הסיכויים. חוסר ההתהפכות נובע מעניין תוכני ולא סטטיסטי.
זו גם הסיבה לכך שאיני מסכים לדברי הש”ך ורעק”א שהבינו שאם לספק השני אין נפ”מ זה נקרא ספק ספיקא שאינו מתהפך. טענתי כאן שבניגוד לדעתם, אני חושב שכל עוד אפשר להסתפק בו זה נחשב ספק ספיקא מתהפך. ספק ספיקא שלא מתהפך זה רק במקרה שלא ניתן בכלל להסתפק בספק השני. כעת תוכלו להבין את ההסבר לכך. אי ההתהפכות יש לה משמעות רק אם היא מצביעה על תלות סטטיסטית, כלומר כשסדר ההסתפקות משנה את ההסתברות לכל אחת מהאפשרויות (לא הנורמות אלא העובדות, הזכרתי כמה פעמים שההסתפקויות הן על העובדות ולא על הנורמות). במקרים של הש”ך ורעק”א ההסתברות לעובדות לא משתנה, ורק הנורמות משתנות (טענתם היא שאין נפ”מ הלכתית לעובדות השונות, אבל הן עדיין שונות). לאור ההסבר שהצעתי כאן ברור שזהו ספק ספיקא מתהפך.
המסקנה היא שרק אם הסיבה לאי ההתהפכות היא סטטיסטית ההיתר על סמך ספק ספיקא הופך למסוכן יותר. אבל לגבי ספק ספיקא שאינו מתהפך (בעובדות ולא בדין), אזי גם אם הסיבה לאי ההתהפכות אינה תלות סטטיסטית עדיין ייתכן שבגלל שבמבנה מסוג כזה יכולה להיות תלות בין האירועים, ההלכה קובעת כלל גורף: בספק ספיקא כזה ניתן לפסוק להיתר. ומכאן שבספיקות שאינם מתהפכים מבטלים עקרונית את ההיתר של ספק ספיקא. כעת כבר לא נכנסים לשאלה האם חוסר ההתהפכות מצביע על תלות סטטיסטית או לא, דלא פלוג.
ועדיין ברור שצריכים להיות מצבים שבהם אי ההתהפכות היא בגלל תלות סטטיסטית, אחרת לכל המהלך הזה אין משמעות. אם אכן יש מקרים כאלה, או אז ניתן לומר שמבטלים את דיני ספק ספיקא כשהוא לא מהפך, גם אם זה לא נובע מתלות. האם באמת יש דוגמאות כאלה? נתבונן בספק ספיקא ממסכת חולין לגבי סכין השחיטה. ראינו שהוא לא מתהפך (אבל גם משם אחד), ושם נראה שחוסר ההתהפכות הוא באמת בגלל תלות בין האירועים. אם ידוע לי שהסכין נפגם לפני רוב השחיטה אז הוא ודאי לא נפגם אחריה. ככל שאני מתקדם על ציר הזמן אני משאיר מאחוריי את כל מה שבא אחרי נקודת הזמן המדוברת. במצב כזה נראה שאי ההתהפכות באמת מצביעה על תלות סטטיסטית. אבל כאמור זהו ספק ספיקא לא מתהפך שהוא גם שם ספק חד. השאלה האם יש דוגמה לספק ספיקא לא מתהפך שאינו משם אחד, ושמתקיים בו גם שאי ההתהפכות נובעת מתלות סטטיסטית? כדי שההסבר שהצעתי יהיה נכון עדיף למצוא גם דוגמה כזאת (אחרת דין ההתהפכות מיותר, כי לדין ‘שם ספק חד’ יש לנו כבר הסבר והוא ודאי קיים). כרגע איני מצליח לחשוב על דוגמה, אבל איני רואה סיבה שלא תהיה כזאת.
[1] הוא בהכרח שקול, כי אם אינו שקול חלים כאן דיני רוב. בזה עסקנו בטור הקודם.
[2] יש כאן הנחה שביאת הנישואין התרחשה אחרי גיל מצוות שלה. כלומר בין הקידושין שהיו לפני גיל שלוש לבין הנישואין חלפו מעל תשע שנים.
[3] ואכן בסופו של דבר רע”א דוחה את ההסבר הזה, שכן לפיו גם אם קידשה פחותה מבת יב (ולא רק בפחותה מבת ג) היינו צריכים לאסור, שהרי אין זה ס”ס המתהפך על פי אותו חשבון. מוכח מיניה וביה ששני הכללים אינם זהים.

