מסקנות על סמך בסיס מידע מצומצם (טור 663)
בס"ד
בטור זה ארצה לגעת בתופעה של הסקת מסקנות מעובדות מפתיעות. לפני כמה שבועות שלח לי מישהו סקר מרתק שהופנה לקהל הרחב בטוויטר:

בסקר נשאלה השאלה שלמעלה, ולמטה מוצגת התפלגות התשובות. מתברר למרבה התדהמה שהתשובות מפולגות בדומה להתפלגות הכדורים במיכל. כלומר 75% מהמשיבים ענו שייצא כדור אדום ו-25% ענו שייצא לבן. תוצאה הפוכה התקבלה עבור התפלגות הפוכה (25 כדורים אדומים ו-75 לבנים), כלומר עדיין נשמרה ההתאמה בין התפלגות התשובות להתפלגות הכדורים במיכל.
אין צורך לומר שהתוצאה הזאת בלתי סבירה בעליל. אם מוציאים כדור אחד והניסוי נערך פעם אחת, אין שום היגיון להניח שהכדור שייצא יהיה לבן. הסיכוי לכך הוא 25%, ואילו לכדור אדום זה 75%. למה להמר על הסיכוי הנמוך?
אם היינו חוזרים על הניסוי הרבה פעמים ומתבקשים בכל פעם להמר, הייתי אולי יכול להבין שיהיה מישהו שירצה להמר על תוצאת המיעוט, שהרי יהיו מקרים שבהם דווקא הוא יצדק. אבל כאמור אצלנו מדובר על ניסוי בודד.
כמו כן, היה לכך מקום כלשהו אם היו מציעים תמורה גבוהה למי שיבחר כדור לבן ויצדק. למשל, אם אומרים שאם בחרת לבן ויצא לבן תקבל 100 ₪, ואם בחרת אדום ויצא אדום תקבל 10 ₪. במצב כזה יש היגיון לבחור בלבן למרות שהוא במיעוט בגלל תוחלת הרווח (אם כי בניגוד למה שאתם חושבים זה ממש לא נכון שאדם רציונלי צריך לבחור בזה. זהו שיקול תוחלת ובניסוי בודד אין שום הכרח לפעול לפי התוחלת. ראו על כך למשל בטור 408 ועוד). אבל כאן אין בכלל הגדרת תמורה לתוצאות השונות, ולכן גם ההסבר הזה אינו רלוונטי.
התוצאה הזאת די הדהימה אותי, ולכן ביקשתי ממי ששלח לי שיבדוק לי האם זה מתקיים גם בהתפלגויות אחרות של כדורים. הניסוי הבא שהוא שלח לי היה זה:

הדיוק קצת קטן יותר, אבל עדיין יש מתאם מובהק למדיי. החריגות הן עניין סטטיסטי צפוי מאד כמובן, אבל המגמה לעומת הניסוי הקודם נראית ברורה למדיי. כשמספר הכדורים יורד (מ-75 ל-65) או עולה (מ-25 ל-35) כך קורה גם לאחוז התשובות. הסיפור מתחיל להישמע מטריד. נראה שאכן יש כאן תופעה לא מובנת שמופיעה באופן עקבי.
הסברים אפשריים
אפשר היה לתלות זאת באחוז הטיפשים באוכלוסייה, אבל לא סביר שאחוז הטיפשים משתנה לפי הניסוי. אם יש רבע מהאוכלוסייה שהם טיפשים הייתי מצפה שהתשובות הטיפשיות תמיד תהיינה רבע, ולא בהתאמה להתפלגות במיכל. כך למשל גם אם יש אחוז מהאוכלוסייה שחושב שמדובר בניסוי חוזר או בניסוי עם תמורה כפי שתיארתי למעלה. גם בשני מקרים כאלה הייתי מצפה להתפלגות קבועה ולא משתנה לפי התפלגות הכדורים במיכל.
משהו כאן נראה לא הגיוני בעליל. טוב, הייתי חייב להמשיך ולבדוק את העניין.
הפתעה
שמתי לב שבכל זאת בניסוי השני המספרים די קרובים לראשון. המגמה אמנם נראית מתאימה לשינוי בהתפלגות הכדורים במיכל, אבל זה יכול להיות מקרי. לכן ביקשתי מהשולח משהו עם התפלגות שונה משמעותית, וזה מה שקיבלתי:
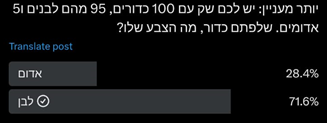
כאן כבר היה שינוי דרמטי בהתפלגות הכדורים, והשינוי בתשובות כמעט לא היה. בוודאי שלא היה לו מיתאם עם השינוי בהתפלגות. הוא נשאר באזור של רבע מול שלושה רבעים.
הפתרון
המשמעות היא פשוטה. יש אחוז קבוע מהאוכלוסייה (משהו כמו 25%-32%) שעונה את התשובה הלא הגיונית. זה יכול לנבוע מטיפשות, או משתי האפשרויות האחרות שהעליתי למעלה (הבנה לא נכונה של הניסוי), אם כי שלושת ההסברים הללו נראו לי בלתי סבירים. סביר יותר מה שהציעה כלתי, קרן, שיש כשלושים אחוז מהאוכלוסייה שהם חכמולוגים שאוהבים לענות תשובה טיפשית רק כדי להתחכם עם השואל. לכן מגלים אותו אחוז בכל התפלגות של כדורים. שתי התוצאות המפתיעות שראינו למעלה נבעו מכך שההתפלגות של הכדורים בשני המקרים הללו הייתה בערך סביב אחוז החכמולוגים באוכלוסייה. ייתכן שמי שהציג את החידה עשה זאת בכוונה, כלומר בחר את שני הניסויים שהתאימו לתופעה שהוא רצה להדגים, או שהוא בדק במקרה את שני המקרים הללו. כך או כך, אין כאן תופעה של התאמה בין התפלגות התשובות להתפלגות הכדורים במיכל.
מסקנה אחרת מהניסויים הללו
למרות זאת בהחלט יש מקום להסיק מהניסויים הללו מסקנה מעניינת. יש אחוז חכמולוגים מסוים באוכלוסייה (לפחות זו שנגישה לטוויטר של אותו אדם וטורחת לענות לשאלות כאלה). זו גם תופעה מחודשת ומעניינת. את זה הייתי ממשיך לבדוק עם סקרים מסוגים שונים (ולא רק מהסוג הזה). מעניין האם זו טיפשות או חכמולוגיות, והאם זה משתנה לפי סוגי השאלות. אגב, בסקרי בחירות יש תופעה ידועה של משיבים שמטעים את הסוקרים. הם כבר למדו לקזז את התופעה הזאת ולכן הם מגיעים לתוצאות כל כך מדויקות. מעניין מה אחוז המטעים הללו לפני הקיזוז. זה גם סוג של חכמולוגים, אם כי מסוג אחר.
שני לקחים ראשוניים
המסקנה הראשונית היא שאסור להסיק מסקנות ממקרים בודדים. התוצאות יכולות להיות מקריות. במובן הזה, גם שלושת הניסויים שהצגתי כאן הם מספר קטן מדיי. לכן המסקנה לגבי החכמולוגים גם היא לא מבוססת דיה.
מסקנה נוספת היא ששינויים קטנים אינם מדד טוב להדגמת תופעה, בפרט אם מדובר על קורלציה בין שני משתנים (התפלגות הכדורים – המשתנה הבלתי תלוי, מול התפלגות התשובות – המשתנה התלוי). שינויים כאלה יכולים להיות מקריים. עדיף לערוך ניסויים בערכים שונים מאד זה מזה של המשתנה הבלתי תלוי (הכדורים). זה מה שמכונה בפילוסופיה של המדע 'גיוון בראיות'. בפרט נכון שאם רואים שינויים קטנים במשתנה התלוי (התשובות, שנעות בין 75% לבין 68%) יש לדאוג לכך שהשינויים במשתנה הבלתי תלוי (הכדורים) יהיו גדולים ביחס אליהם (ולא די ב-75 מול 65).
הסקת מסקנות על סמך בסיס מידע מצומצם
הבעיה העיקרית בהסקת מסקנות על בסיס מידע מצומצם היא שבסיס מצומצם מאפשר מנעד רחב של תוצאות. עמדתי על כך בטור 38.
בין היתר, ראינו שם לדוגמה את שיעור התמותה מסרטן כליה במחוזות שונים בארה"ב. מסקר שנערך התברר שהאחוזים הגבוהים ביותר התקבלו באזורים כפריים במערב התיכון. ניתן היה להציע לכך הסברים שונים (נגישות נמוכה לבריאות, השכלה נמוכה וכדומה), אלא שאז התברר שהאחוז הנמוך ביותר של תמותה התקבל גם הוא באזורים כאלו. ההסבר לכך הוא מאד פשוט. אלו היו האזורים הדלילים ביותר באוכלוסייה, ולכן שם חוק המספרים הגדולים לא עובד. באזור כזה ניתן לקבל תוצאות שונות מאד מהממוצע. חשבו על אזור שיש בו תושב אחד. אם הוא חולה בסרטן כליה אז יש לנו 100% תחלואה. גם אם יש לנו הרבה אזורים שבכל אחד מהם עשרה אנשים, יהיו מהם כמה כאלה שיהיו בהם שלושה חולים בסרטן כליה, כלומר שיעור תחלואה של 30%. מאידך, יהיו אזורים כאלה שלא יהיה בהם אף חולה, והם ייחשבו בריאים במיוחד.
דוגמה נוספת שהובאה שם הייתה בדיקת ההצלחה בלימודים בבתי ספר שונים, שהניבה תוצאות דומות: שיעורי ההצלחה הגבוהים ביותר התקבלו בבתי ספר קטנים. ההסבר היה מתבקש: יש שם טיפול יחידני, ההורים אמידים (יש להם כסף לשלוח ילדים לבי"ד קטן) וכדומה. בעקבות הסקר הזה, קרן גייטס השקיעה סכומי עתק כדי להקטין את מספר התלמידים בבתי הספר. אלא שאז התברר ששיעורי ההצלחה הנמוכים ביותר התקבלו גם הם בבתי ספר קטנים. ושוב, יש לכך הסברים. מגוון האפשרויות שמציע בי"ס כזה הוא קטן יותר מזה שמוצע בבי"ס גדול. אבל שני סוגי ההסברים הללו אינם עולים בהכרח מהממצאים (אם כי הם יכולים להיות נכונים כשלעצמם). גם כאן ההסבר הוא שבמספר קטן של תלמידים יתקבלו תוצאות מגוונות יותר ורחוקות יותר מהממוצע. בבתי ספר גדולים, בגלל חוק המספרים הגדולים, התוצאות יהיו קרובות לממוצע.
לקח חשוב נוסף שעולה מכאן הוא שאד הוק אפשר להסביר הכל. תן לי תופעה ואציע לך הסבר. כל עוד אינך בודק את ההסבר הזה על מגוון רחב של עובדות (ערכים שונים של המשתנה הבלתי תלוי), אין להסברים הללו משמעות רבה. אני מזכיר לכם את ההסברים שהצעתי לתוצאות ניסוי הכדורים. כאר ההסבר הזה נשמע לנו הגיוני מאד, המצב מסוכן עוד יותר. במקרה כזה אנחנו הולכים שבי אחרי ההנחות האפריוריות שלנו ומאמצים את ההסבר הזה, ואף מייחסים אותו לממצאים סטטיסטיים. כעת ההיגיון שלנו כבר נוצק בסלע. הוא מדעי.
דניאל כהנמן מכנה זאת "חוק המספרים הקטנים". ממצאים על בסיס קטן של עובדות וניסויים שמתאימים להסבר שנראה לנו הגיוני אפריורית, הופכים בעינינו לחוק טבע ולעובדה מוצקה. כך חייל שניצל בזכות ספר תהילים שהיה לו בכיס ועצר את הכדור שנורה עליו, משוכנע שיד ההשגחה עשתה זאת. הוא כמובן לא טרח לבדוק כמה אנשים ניצלו בזכות ספרים אחרים, או להיפך, נפגעו בגלל שהיה להם ספר תהלים בכיס שהסיט את הכדור ישירות ללב. לחלופין, כמה אנשים לא ניצלו למרות שהיה להם ספר תהלים בכיס. חשוב על אם שחשה תחושה קשה בדיוק ברגע שבנה החייל נפגע בחזית, והיא בטוחה שמדובר בטלפתיה או אמפתיה אימהית מיוחדת. היא לא טרחה לבדוק כמובן כמה פעמים היו לה תחושות כאלה כשבנה לא נפגע, וכמה אימהות לא חשו מאומה כשבנן נפגע או לא חשו כשהוא כן נפגע וכדומה. כל אלו הן דוגמאות לחוק המספרים הקטנים.
עד כאן עסקתי בהסקת מסקנות על בסיס מידע מצומצם. ההנחה הייתה שהאדם שהציג את הניסויים הללו בטוויטר עשה זאת בתום לב, ובמקרה יצאו לו ממצאים מפתיעים. במקרה יצא שהוא בדק מצבים כאלה שהתאימו לאחוז החכמולוגים באוכלוסייה. אבל ייתכן גם שאותו אדם ערך הרבה ניסויים ובחר להציג דווקא את אלו שהתאימו לתזת ההתאמה. זהו כשל שמבוסס גם הוא על המנעד של מדגמים קטנים, ומאפשר לנו לבחור את הבסיס העובדתי שלנו באופן מגמתי. זה מה שמכונה קטיף דובדבנים' (cherry picking), כשל שכבר נגעתי בו בעבר (ראו למשל בטור 640, בשו"ת כאן ועוד).
קטיף דובדבנים
הכשל שקרוי קטיף דובדבנים הוא בחירה מגמתית של קבוצת עובדות מתוך עובדות רבות יותר כדי לבסס תזה שאנחנו חפצים בה. חשבו על אותו בעל דף טוויטר שרוצה לקדם את התזה של קשר בין התפלגות התשובות להתפלגות הכדורים. הוא ערך כמה וכמה ניסויים בכל מיני מצבים של כדורים במיכל. כמעט בכולם התפלגות התשובות היא סביב 30% חכמולוגים מול 70% משיבים רגילים. כעת הוא בוחר את הניסויים שסביב 30-70, ומתוכם הוא בוחר את אלו שבהם התוצאות לגבי התשובות הכי קרובות להתפלגות הכדורים במיכל, באופן שידגים מגמתיות בכיוון הרצוי (כמו בניסוי השני כאן למעלה), ואז מציג את המדגם החלקי הזה של הניסויים בפני הציבור. זה יכול לשכנע רבים מאתנו שאכן קיים מתאם בין התפלגות התשובות להתפלגות הכדורים במיכל.
הבחירה הזאת מכונה 'קטיף דובדבנים' מפני שגם פועל שעוסק בקטיף מתבקש על ידי בעל הבית לקטוף את הדובדבנים הטובים יותר. יתר על כן, כשהוא יציג את הפירות שקטף בפני אחרים הם יסיקו שמדובר במטע מעולה שמניב פירות משובחים, כשבעצם יש עוד פירות רבים באיכות פחות טובה שנותרו על העץ. הכשל של 'קטיף דובדבנים' הוא בחירת העובדות (=הפירות) הרצויות לנו מתוך כלל העובדות (=הפירות). מסקנה שמוסקת על בסיס מדגם מוטה ומגמתי שכזה כמובן אינה נכונה.
אנשים שעוסקים בפסאודו מדע (כמו רפואה אלטרנטיבית. ראו בטור 38 הנ"ל) ותיאוריות קונספירציה נוהגים להשתמש בקטיף דובדבנים. הם בוחרים ציטוטים או מקרים מוצלחים כדי לאשש תזות שונות. כשהתזה נתונה מראש אין שום בעיה למצוא נתונים שיאששו אותה. אורן זריף, ניר בן ארצי, האורקך מדלפי, עתידנים אקדמיים כמו דוד פסיג, וכל מיני שרלטנים ומחוללי קסמים, רבנים ואחרים, מתבססים על קטיף דובדבנים כזה. יש כמה מקרים שבהם נבואתם התממשה, פשוט בגלל הסטטיסטיקה, ואלו בונים להם תהילת עולם כקוסמי על, כאשר אנשים לא מודעים לכך שיש לא פחות מקרים שבהם הם נכשלו. רצוי גם להתבטא באופן עמום דיו כך שהתזה לא ניתנת להפרכה. כך תמיד ניתן יהיה להתאים את מה שקרה לתזה הדרושה.
בחר מספר
הבאתי כאן בעבר את הדוגמה מהספר בחר מספר, מאת ג'ון ורדון. אני מקבל מעטפה ובתוכה מכתב ועוד מעטפה קטנה. במכתב פונים אליי ואומרים לי לבחור מספר בין 1 ל-1000. לאחר מכן מבקשים ממני לפתוח את המעטפה הקטנה ובה אמצא בדיוק את המספר שבחרתי. הכותב ממשיך ואומר לי שאם אווכח שיש לו כוחות על, אזי אם ארצה אוכל לשלוח לו 10,000 דולר הוא יהפוך אותי למיליונר. טוב, בגיחוך על שפתיי אני בוחר מספר, למשל 712, וכשאני פותח את המעטפה לתדהמתי אני מוצא בה בדיוק את המספר הזה. טוב, אחסוך לכם את המחשבה. אחרי החקירה התברר שהכותב שלח עשרת אלפים מעטפות כאלה לעשרת אלפים נמענים, ובתוך כל אחת מהן הופיע מספר מקרי בין 1 ל-1000. אתם מבינים שבממוצע הוא יקלע בעשר מהפעמים לבחירה של מקבל המכתב. כך שהוא יכול להרוויח 100,000 דולר טבין ותקילין, על לא עוול בכפו. מקבל המכתב כמובן בונה את התיאוריה שלכותב יש כוחות על, על בסיס מדגים מגמתי (דוגמה אחת). אם היה יכול להסתכל על כלל העובדות היה מבין שאין שום בסיס לתיאוריה שלו. במקרה זה, הכותב הצליח להציג בפני חלק מהנמענים מדגם מוטה לטובת התזה שיש לו כוחות על.
לגלות עוד מהאתר הרב מיכאל אברהם
Subscribe to get the latest posts sent to your email.


אחרי הרף שהרב הציב במאמר הקודם ישבתי וציפיתי, דרך אגב בסקרים ביוטיוב טוויטר וכל מראין בישין, יש אפשרות לשנות את בחירתך אחרי שאתה יודע את תוצאות הסקר הנוכחיות, לכן לא פעם אנשים "מתקנים" את בחירתם אחרי שראו את התוצאות.
זה, וגם שלפעמים אפשר לראות את תוצאות הסקר לפני שענית והן נותנות לך רעיונות.
אהבתי את האזכור של פסיג. אכן, יש מן המשותף ב'נבואות' שלו ושל ניר בן ארצי. שניהם מדקלמים שורה של אסונות גנריים: מלחמה, רעידת אדמה, מגפה. ואז הופה, משהו מתוך זה מתגשם, וה'עתידן' מקבל כותרת "האיש שחזה את הפלישה הרוסית לאוקראינה ".
מה זה שונה מהטיעון הפיזקו-תאולגי,
אנחנו מכירים רק עולם אחד ובונים עליו תאוריה רבתית זה ממש קטיף דובדבנים. ומה עם כל האי סדר שיש בבריאה?
אין לי מה לעשות עם ניסוח רשלני כל כך. נסח שאלה מוגדרת יותר אם אתה רוצה לדון.
הנחה א':
לא ניתן להפיק מידע על סמך קבוצה קטנה מידיי של מאורעות.
הנחה ב':
אנחנו מכירים רק עולם אחד.
הנחה ג':
מסקנה מעולם אחד הוא קבוצה קטנה כדי לדון על אפשרויות של ליצירת עולמות.
מסקנה:
לא ניתן להסיק כלום מקיום העולם שלנו.
א. ניתן בהחלט להפיק מידע מקבוצה קטנה של מאורעות. תלוי איזה מידע.
ב. נכון.
ג. שטויות. לא הסקתי את המידע הזה מהעולם שאותו אני מכיר. ההנחה שדבר מורכב לא נוצר מעצמו היא הנחה של התבונה ולא תוצאה של ניסיון.
ד. כנ"ל.
אפשר תרגום לעברית?
אתה באמת לא הבנת או שלא רצית להבין? זה נראה לי שאלה טריוואלית..
לדעתי התשובות ה"שגויות" נבעו מהתקוממות של חלק מהקוראים על הניסוח המוחלט: "מה צבע הכדור". כאילו שניתן לדעת.
אלה חכמולוגים לוחמי צדק 😉
מעניין האם בניסוח שונה כמו למשל "מה סביר להניח שצבע הכדור" וכד', אחוז החכמולוגים היה שונה.
מאמר מצוין. בהיר ומרתק תודה
יתכן ואולי יש עוד סוג אנשים שעשויים לחשוב שהשואל מנסה לבלבל כשהוא שואל שאלה שנראית פשוטה מדי. ייתכן שהם יחשבו שיש כאן 'קאץ' ולכן התשובה הנכונה היא דווקא מה שנראה לא הגיוני.
כן, אבל הייתי מצפה שישקיעו עוד שנייה מחשבה וינסו לחפש מדוע התשובה ההיא היא הנכונה. כשלא ימצאו יענו מה שנכון. טוב, כל אלו ספקולציות והן לא חשובות לעצם הדיון שלי.
אני פעיל בטוויטר ואני זוכר את הסקר המדובר.
אני זוכר שכשעניתי על הסקר הבנתי אותו לא כ'חידה' ששואלת על מה עדיף להמר, אלא כ'אתגר' שהמצייץ מאתגר את הקהל לבחור תשובה בסקר ככה שהתוצאה תהיה לפי ההתפלגות הרצויה.
יכול להיות שטעיתי, אבל גם קראתי את התגובות וייתכן שהרושם שלי מבוסס גם עליהן, אני לא זוכר בדיוק.
"וכמה אימהות לא חשו מאומה כשבנן נפגע או לא חשו כשהוא כן נפגע וכדומה."
אחרי ההתלוצצות על החייל שניצל בזכות ספר התהלים, לא הבנתי מה אתה רוצה לומר. במה שונה "אימהות שלא חשו מאומה כשבנן נפגע" מאלו ש"לא חשו כשהוא כן נפגע"?
ההתייחסות לדוד פסיג היא מעניינת. הוא טוען שהתחום שלו בונה מודל סטטיסטי שמתבסס על דפוסים שמוסקים מההיסטוריה של ההתנהגות האנושית.
והוא לא טוען שזו אמת מוכרחת אלא רק סבירה מאוד, ובכל אופן הוא אומר שהמטרה היא לעודד את האנושות לנקוט בצעדים שירחיקו אותנו מהסטטיסטיקה שהוא מצא.
למה זה בעיניך דומה לשרלטנות נפוצה? זה דווקא נשמע רציונלי הרבה יותר, גם אם לא מדעי במלוא מובן המילה.
כפי שעניתי לך בשאלה מקבילה: זה אכן נשמע מופלא, הבעיה היא רק העובדות (איזה עולם מעצבן. כל התיאוריות ההרמוניות מתנפצות לקרקע העובדתית העקשנית). התחזיות שלו שוות קדחת. התירוץ שהוא לא אומר שזה הכרחי הוא מריחה כמובן. אף אחד לא מצפה להכרחיות. מה שאני מצפה הוא למדדים סטטיסטיים שיראו שהתחזיות שלו טובות יותר משלי או שלך. להערכתי לא תמצא כאלה, ואם תמצא גם הם מוטים. התחזיות שלו גם בד"כ לא אומרות מאומה, סוג של כרפל שתמיד ניתן להצדיק. פטנט שימיו כימי האורקלים מדלפי.
בדיוק הבוקר תהיתי (אז מי אמר שאין השגחה פרטית?!), מי חכם יותר, אורן זריף או דוד פסיג. שניהם עושים בדיוק אותו דבר, אלא שפסיג הוא שכיר וזריף הוא עצמאי. זריף אמנם מרוויח יותר מהכישופים ואחיזות העיניים שלו, אבל פסיג קיבל דרגה ומעמד של פרופסור עם ביטחון תעסוקתי בקתדרה על שם האורקל מרמת גן, באמצעות אותם כישופים ואחיזות עיניים.