על אבדוקציה ומתמטיקה (טור 537)
בס"ד
בשיעוריי על לימוד מהניסיון עמדתי על היחס בין אינדוקציה לאבדוקציה. בעקבות השיעורים, שלח אליי יהודה את המייל הבא:
נתקלתי במאמר שמדגים שימוש כושל באינדוקציה, ואיך אבדוקציה יכולה להציל את המצב. המאמר מצורף (ראה איור 2 בתוכו). זאת ברוח הסדרה הנוכחית שאני צופה בה ב- YouTube.
קראתי את המאמר ומאד נהניתי, וחשבתי שזו הזדמנות לגעת קצת בסוגיות האבדוקציה, ולהסביר מדוע לדעתי המאמר הזה אינו דוגמה טובה לזה. הבנת פרטי המאמר והטור דורשת ידע מתמטי מסוים, ולכן אכתוב את הטור באופן שיאפשר למי שמעוניין לא להיכנס לפרטים המתמטיים.
מהי אינדוקציה?
אנחנו רגילים לחלק את דרכי ההיסק בלוגיקה לשלושה סוגים: דדוקציה, אינדוקציה ואנלוגיה. דדוקציה היא היסק מהכלל אל הפרט, כלומר מהכלל "כל X הוא Y" ניתן לגזור ש-a שהוא פרט בתוך X הוא גם Y. לדוגמה, אם X הוא קבוצת בני האדם, ו-Y הוא קבוצת בני התמותה, אזי פרט a שהוא אדם (נכלל ב-X) בהכרח הוא גם בן תמותה (נכלל ב-Y).
כעת עולה השאלה איך הגעתי להכללה "כל X הוא Y"? הרי לא יכולתי לראות את כל בני האדם ולוודא שאכן כולם בני תמותה. בדרך כלל מגיעים לזה בדרך של אינדוקציה (מדעית): ראיתי בעצמי שכמה פרטים כאלה היו בני תמותה, ומכאן אני עושה הכללה שכנראה אלו לא היו סתם מקרים בעלמא אלא מדגם מייצג שמדגים בפניי את החוק הכללי שלפיו כל בני האדם הם בני תמותה.
יש לציין שלא מדובר כאן באינדוקציה מתמטית. במתמטיקה, אינדוקציה היא טכניקת הוכחה של טענה ביחס לאינסוף מקרים. אם אני מוכיח אותה למקרה הראשון, ומוכיח שאם היא נכונה למקרה ה-K אזי בהכרח היא נכונה למקרה ה-K+1, ואז ניתן לראות בזה הוכחה שהטענה נכונה לכל המקרים. מכאן תוכלו לראות שאינדוקציה מתמטית היא סוג של דדוקציה, כלומר שמסקנתה היא וודאית ונכונה בהכרח (יש לנו הוכחה עבורה), אחרת היא לא הייתה שייכת למתמטיקה.[1] אינדוקציה במובנה הרגיל, זו שבה אנחנו עוסקים כאן, מופיעה במדע ולא במתמטיקה. כאן לא מדובר בהוכחה אלא בהיסק שגוזר מכמה פרטים חוק כללי.
נשוב כעת לאינדוקציה מדעית. כפי שהראה כבר דייוויד יום, אינדוקציה כזאת היא הליך בעייתי. גם אם ראיתי שהתופעה קיימת במספר סופי של מקרים, כיצד אוכל לדעת שהתופעה הזאת נכונה לכל המקרים מהסוג הזה? לחלופין, מכל אוסף של מקרים ניתן לגזור אינספור חוקים כלליים שונים. איך אני יכול לדעת מי מהם הוא החוק הכללי הנכון?
התשובה היא שאין לנו דרך לדעת זאת בוודאות. המקרים שבהם צפינו כשלעצמם לא יכולים לברור בין ההכללות השונות, שהרי מדובר בהכללות שכל אחת מהן מתאימה לכל המקרים שראינו. אבל האינטואיציה מסייעת לנו לראות שהכללה מסוימת היא סבירה יותר (אולי לפי הפשטות שלה, או קריטריונים אינטואיטיביים אחרים). דייוויד יום, שערער על האינדוקציה, הניח שאם אין לנו וודאות ביחס להכללה הנכונה אזי אין לנו אפשרות לטעון שהיא נכונה יותר מחברותיה. הוא טען שזוהי ספקולציה שנובעת ממבנה החשיבה שטבוע בנו, אבל אין לגזור מכאן מאומה על העולם כשלעצמו. אבל כפי שכתבתי לא פעם בעבר, לדעתי הוא טעה בזה, שכן ודאות אינה תנאי נדרש לידיעה. יכולות להיות ידיעות לא ודאיות. למעשה, כל הידיעות שלנו הן כאלה (למעט טענות טאוטולוגיות).
אם כן, אינדוקציה היא היסק שלוקח סט של מקרים פרטיים ויוצר מהם חוק כללי, כך שהם מקרים פרטיים של החוק הזה (ניתן לגזור אותם ממנו בדדוקציה)[2]. בלשונו של פילוסוף המדע קרל המפל, זוהי הסכימה הדדוקטיבית-נומולוגית, שבמסגרתה החוק הכללי מהווה הסבר למקרים הפרטיים אם ניתן לגזור אותם ממנו בדדוקציה. הדרך מהמקרים לחוק הכללי היא אינדוקציה, הדרך ממנו אליהם היא דדוקציה. מתוך כל סט של מקרים ניתן לגזור כמה הסברים דדוקטיביים-נומולוגיים, והברירה של אחד מביניהם נעשית על ידינו משיקולים של סבירות, פשטות וכו' (זה כבר לא הליך אמפירי טהור).
מהי אבדוקציה?[3]
בבסיס האינדוקציה שאנחנו עושים תמיד נמצאת תיאוריה כלשהי. חשבו על שאלה ממבחן פסיכומטרי, שמציגה בפניכם את סדרת המספרים הבאה, ומבקשת מכם לכתוב את הבא בתור:
3, 5, 7, ?
אני מניח שרובכם תכתבו שם 9. אבל אני מציע המשך אחר לסדרה: 11. נכון או לא? זה תלוי בהסבר שתציעו לסדרה הזאת: אם מדובר בסדרת האי-זוגיים, אזי ההמשך הנכון הוא 9, אבל אם מדובר בסדרת הראשוניים אזי ההמשך הנכון הוא 11 (כי 9 אינו ראשוני). מי צודק? אין כאן צודק או טועה, שכן שתי התשובות נכונות באותה מידה. בבסיס כל אחת מהן נמצאת תיאוריה שונה, אבל שתי התיאוריות מתאימות למקרים שבהם צפינו, ולכן אין דרך להכריע ביניהן רק מתוך המספרים הידועים לנו בסדרה. אלו שתי פרשנויות אפשריות לסדרה, על אף שהן נותנות לנו ניבוי שונה למספר הבא.
כך בדיוק קורה לא פעם במדע. יש לנו אוסף של תצפיות על מקרים שאותם פגשנו, ואנחנו מחפשים הכללה שלהם לחוק כללי כלשהו (שיאמר לנו מה יקרה במקרה אחר, שבו טרם צפינו). ההכללה הזאת היא אינדוקציה, אבל כפי שניתן לראות כאן, יש כמה אפשרויות להכללה כזאת. מי שיכריע בין האפשרויות הוא התיאוריה שעומדת ביסודן (ראשוניים או אי-זוגיים). התיאוריה היא שקובעת את החוק הכללי. המעבר מאוסף של עובדות לחוק כללי הוא אינדוקציה, המעבר מאוסף העובדות הזה לתיאוריה קרוי אבדוקציה (בעקבות הפילוסוף האמריקאי צ'רלס פרס).
כאשר אנחנו מבצעים הכללה כלשהי, בחיים או במדע, לא תמיד אנחנו מודעים להנחות סמויות שעומדות ביסודה, אבל תמיד ישנן שם הנחות כאלה. לפעמים הכללה כלשהי נראית לנו טבעית ומתבקשת ולכן ברור לנו שזהו החוק הכללי, ואנחנו לא שמים לב שבמובלע הנחנו כאן תיאוריה כלשהי, כלומר עשינו אבדוקציה סמויה. כך הסטודנט שיכתוב 9 כתשובה לשאלה הנ"ל, אפילו לא ייתן לעצמו דין וחשבון ולא תמיד יהיה מודע לכך שהוא מניח הנחה כלשהי. מתוך כך הוא עלול להיות עיוור לאפשרות שייתכנו גם המשכים אחרים (כמו 11 למשל. אגב, יש עוד אינספור המשכים אפשריים אחרים). אם הוא יהיה מודע לכך שבבסיס האינדוקציה שלו מונחת אבדוקציה, הוא יהיה ער ורגיש יותר לאפשרויות אלטרנטיביות כמובן.
דוגמאות: פרשנות שגויה לקורלציות
ניתן להדגים זאת על מקרים של קורלציות שמובילות למסקנות שגויות. כך לדוגמה ניתן לטעון שלא כדאי לעשות דיאטה, שהרי כל מי שעושה דיאטה הוא שמן. גם אם נכון שיש קורלציה בין דיאטה לשומן (אלו העובדות), ישנה כאן טעות בתיאוריה שמהווה הסבר לקורלציה הזאת. לא הדיאטה גורמת לשומן אלא השומן לדיאטה. לכן המסקנה שכדאי להימנע מדיאטה אינה נכונה. הצענו כאן הכללה לגבי הקשר בין דיאטה לשומן, אבל היא הייתה מבוססת על התיאוריה הלא נכונה, כלומר טעינו באבדוקציה שלנו וזה הוביל לטעות במסקנה (שמקבילה לאינדוקציה).
דוגמה אחרת לכך היא מכתב שכתב פרופ' מהטכניון למערכת עיתון לפני שנים, שבו הוא המליץ שמדינת ישראל תגביר את ההשקעה בהשכלה הגבוהה, שכן ישנה קורלציה בין השקעה בהשכלה הגבוהה לבין תוצר לאומי גבוה. גם אם נכון שקיימת קורלציה כזאת, המסקנה שלו אינה הכרחית. היא תלויה בהסבר לקורלציה (האבדוקציה), שיכול להיות לפחות אחד משניים: 1. השקעה גדולה בהשכלה הגבוהה מגדילה את התוצר (זה ההסבר שהוא הניח). 2. תוצר גבוה מביא להשקעה גדולה בהשכלה הגבוהה (כי מדינה שיש לה כסף יכולה להשקיע אותו במותרות). אין דרך להכריע בין שתי האפשרויות הללו רק מתוך העובדות שהוא תיאר (כדי להכריע צריך לעשות רגרסיות). אם כן, הכללות או מסקנות שאנחנו מסיקים באופן טבעי מתוך נתונים או תצפיות, תלויות בתיאוריה. ההכללה שהיא תוצר של אינדוקציה, תמיד מבוססת על תיאוריה שנוצרת על ידי אבדוקציה. אבדוקציה שונה תיתן לנו אינדוקציה שונה.
דוגמה נוספת: ניתוח של 'קל וחומר'
דוגמה נוספת למשמעותה וחשיבותה של אבדוקציה ניתן לראות בניתוח של היסק קל וחומר.[4] חשבו על הקל וחומר הבא (שמבוסס על משנת ב"ק כד):
| מזיק / רשות | רה"ר | חה"נ |
| שן ורגל | 0 | 1 |
| קרן | 1 | ? |
טבלה 1
בטבלה 1 יש לנו שלושה נתונים (שראינו בתורה. אלו הנתונים ה'אמפיריים'): נזקי שן ורגל (=שו"ר) פטורים ברה"ר, אבל חייבים בחצר הניזק. נזקי קרן חייבים ברה"ר (לצורך הפשטות אני מתעלם כאן מזה שהחיוב הוא חצי נזק). השאלה היא לגבי דין שאינו כתוב בתורה (ולכן אינו ניתן לתצפית), מה דינם של נזקי קרן בחה"נ? כפי שניתן לראות במשנה שם, עולים שני טיעונים שמוכיחים שנזקי קרן בחה"נ חייבים מתוך הטבלה שלמעלה:
- טיעון העמודות. משני הנתונים בעמודה הימנית רואים שקרן קל יותר לחייב מאשר שו"ר. כעת עוברים לעמודה השמאלית, ומסיקים שאם נזקי שו"ר חייבים בחה"נ קל וחומר שקרן (שחמורה מהם) תהיה חייבת שם. מש"ל. ההנחה בבסיס הטיעון הזה (כלל ההיררכיה) היא שחיובי קרן חמורים מחיובי שו"ר.
- טיעון השורות. משני הנתונים בשורה העליונה רואים שבחה"נ קל יותר לחייב מאשר ברה"ר. כעת עוברים לשורה התחתונה, ומסיקים שאם קרן חייבת ברה"ר ודאי שתהיה חייבת בחה"נ. ההנחה בבסיס הטיעון הזה היא שחיובי חה"נ חמורים יותר (קל יותר לחייב) מאשר חיובי רה"ר.
על פניו אלו שני טיעונים שונים ובלתי תלויים. כל אחד מהם מבוסס על הנחה אחרת, למרות שהם מגיעים לאותה מסקנה. כדי לראות זאת, חשבו על פירכא על טיעון העמודות. פירכא כזאת מציגה רשות שלישית, שבה שו"ר יהיו חייבים וקרן לא. נניח לדוגמה שבנזק שנגרם על אי בים קרן פטורה ושו"ר חייבים. אנחנו מקבלים את הנתונים בטבלה 2:
| מזיק / רשות | רה"ר | חה"נ | אי |
| שן ורגל | 0 | 1 | 1 |
| קרן | 1 | ? | 0 |
טבלה 2
מדוע זוהי פירכא? מפני שמהעמודה השמאלית ניתן להסיק שההיררכיה שהנחנו בין קרן לשו"ר אינה הכרחית. אבל לכאורה גם אחרי הפירכא טיעון השורות נותר על כנו, שכן הוא אינו מניח שום היררכיה בין המזיקים אלא בין הרשויות, והפירכא הזאת אינה תוקפת את ההיררכיה הזאת.
לעומת זאת, פירכא על טיעון השורות תציג בפנינו מזיק שלישי שחייב ברה"ר ופטור בחה"נ. נניח לדוגמה שנזקי אוזן הם כאלה, ונקבל את טבלה 3:
| מזיק / רשות | רה"ר | חה"נ |
| שן ורגל | 0 | 1 |
| קרן | 1 | ? |
| אוזן | 1 | 0 |
טבלה 3
שורת הפירכא מראה לנו שההיררכיה בין רה"ר לחה"נ אינה הכרחית, וכך תוקפת את טיעון השורות. אבל ההנחה של טיעון העמודות לכאורה נותרת על כנה.
אם כן, היינו מצפים שבספרות התלמודית כאשר מוצגת פירכא על קו"ח התגובה תהיה 'סיבוב' של הקו"ח והשארת המסקנה על כנה. אבל בכל ספרות חז"ל ובמפרשים לא מוצאים זאת. אחרי שמוצגת פירכת שורה או עמודה הגמרא מסיקה שהקו"ח נפל.[5] לכאורה ישנה כאן הנחה ששני הטיעונים הללו הם שני ניסוחים שונים של אותו טיעון. השאלה היא מדוע. ניתן לראות את הסיבה לכך בתיאוריה שעומדת בבסיס ההיסק של הקו"ח. היסק הקו"ח הוא סוג של אינדוקציה (או בעצם אנלוגיה), אבל ביסודו יושבת אבדוקציה, כלומר תיאוריה שמסבירה אותו. כאשר מבינים את זה ומודעים לזה, הקושי נעלם מאליו.
כדי לראות זאת, נחזור לטבלה 1 ונתבונן תחילה בטיעון העמודות. העמודה הימנית מראה לנו שלקרן יש מאפיין כלשהו שבגללו יש לחייבה יותר מאשר שו"ר. נסמן אותו באות α (אלפא), ונניח שקרן חמורה יותר משו"ר מפני שיש בה את המאפיין הזה בעוצמה גבוהה יותר מאשר בשו"ר. אז אם לשו"ר יש אותו בעוצמה α לקרן יש אותו בעוצמה 2α. אלא שאין די בכך כדי להבין את הנתונים בטבלה. כדי להסביר את הנתונים עלינו להניח בנוסף לכך, שכדי לחייב ברה"ר דרוש מזיק שניחן במאפיין הזה בעוצמה 2α, ולכן שו"ר לא מתחייב שם וקרן כן. ומה קורה בחה"נ? שם יתחייב כל מזיק שניחן בעוצמה α בלבד (אחרת שו"ר לא היה חייב שם). כלומר כדי להסביר את הקו"ח של המזיקים (העמודות) חייבים להוסיף הנחה ביחס לרשויות (השורות). לא רק זה, ההנחה שהוספנו מערבת בהכרח את אותם פרמטרים שהיו מעורבים ביחס למזיקים, אחרת המאפיין הזה במזיקים לא היה רלוונטי לחיובם ברשויות השונות.
שימו לב מה קיבלנו: כדי להסביר את הנתונים בטבלה, לא די לנו לקבוע היררכיה בין המזיקים, אלא בהכרח אנחנו צריכים לקבוע את אותה היררכיה בין הרשויות. יתר על כן, ההיררכיה ביניהן גם היא מתוארת במונחי אותו פרמטר α. למרבה הפלא, ההנחה של טיעון העמודות שקובעת היררכיה בין המזיקים מאלצת אותנו במובלע להניח את אותה היררכיה עצמה בין הרשויות. אבל אם כך, כאשר נפגוש פירכת עמודה, שמערערת את ההיררכיה בין המזיקים, היא תערער מתוך כך גם את ההיררכיה בין הרשויות (שכן אחרי הפירכא שוב אין סיבה להניח גם אותה). זוהי הסיבה לכך שהתלמוד מניח שפירכת עמודה פורכת גם את טיעון השורות. כמובן שכך גם יהיה לגבי טיעון השורות ופירכת שורה, שתפרוך גם את טיעון העמודות.
ההיסק של הקו"ח, פועל משלושת הנתונים בטבלה ומסיק מהם את הנתון הרביעי (החסר). זוהי הסקה במישור של העובדות, כלומר משהו שמקביל לאינדוקציה (או אנלוגיה, במקרה הזה). אבל ברקע, גם אם לא שמנו לב, מונחת תיאוריה (ההנחה בדבר מאפייני α של המזיקים ושל הרשויות), והיא שעומדת גם בבסיס הנתונים וגם בבסיס ההיסק. אם כן, עשינו כאן אינדוקציה שמבוססת על אבדוקציה סמויה. הפירכא, באם קיימת כזאת, מראה לנו שהאבדוקציה בה השתמשנו אינה נכונה, וממילא גם האינדוקציה (ההסבר של כלל הנתונים בטבלה) והמסקנה שמוסקת במסגרתה נופלות. חשבו על פירכא לטיעונו של הפרופסור הנ"ל שמראה מדינה שלא משקיעה בהשכלה הגבוהה ויש לה תוצר גבוה (או שכן משקיעה והתל"ג שלה נותר נמוך). פירכא כזאת מראה שאין רלוונטיות בפרמטר המסביר (השקעה בהשכלה הגבוהה) כדי להבין את המוסבר (התוצר).
אבדוקציה במדע: קרינת גוף שחור
כך קורה גם במדע. יש בפנינו אוסף של עובדות מתצפיות שונות, ואנחנו מחפשים חוק כללי שיסביר אותן. הדרך להגיע להכללה כזאת היא אינדוקציה. אבל האינדוקציה רק נותנת לנו תיאור סגור של מה שיקרה באינסוף מקרים אחרים, אבל ללא הסבר. כדי להבין את התופעות הללו, ודרך זה גם לוודא שהאינדוקציה שעשינו נכונה, עלינו לעשות אבדוקציה, כלומר לחפש את התיאוריה שעומדת בבסיס העובדות הללו. התיאוריה הנכונה כמובן תניב את החוק הכללי הנכון. ההכללה המדעית נותנת לנו נוסחה שמתארת מה יקרה בכל המצבים והמקרים, אבל התיאוריה היא המסגרת המושגית שמסבירה את הנוסחה ומצדיקה אותה.
בהיסטוריה של המדע מוכרים לנו מצבים שבהם נעשתה אינדוקציה לפני האבדוקציה, כאשר מכלילים את העובדות מהתצפית ויוצרים מהן חוק כללי, נוסחה או משוואה. החוק נותן לנו את התוצאות שצפויות להתקבל במקרים אחרים שבהם טרם צפינו. עדיין אין לנו הסבר מדוע זוהי הנוסחה וכיצד הגענו מהתצפיות לנוסחה הזאת (ואולי יש אלטרנטיבות אחרות). בשלב הזה יש בידינו תיאוריה פנומנולוגית, כלומר תיאור כללי של אינספור עובדות שהוא הכללה של העובדות הידועות לנו. כאשר נמצא תיאוריה שתסביר את הנוסחה הכללית, אם אכן נמצא כזאת, היא תעגן טוב יותר את הטענה שהנוסחה הזאת היא ההכללה הנכונה. תיאוריה כזאת כוללת בתוכה עקרונות ומושגים ומכלול של קשרים ביניהם, שבמסגרתה ניתן להראות שהחוק הכללי שאליו הגענו באינדוקציה הוא החוק הנכון. אם לא נמצא תיאוריה כזאת, עולה חשד שהאינדוקציה שלנו (המשוואה) לא הייתה נכונה. נדגים זאת דרך מציאת ההסבר לקרינת גוף שחור.
כבר בסוף המאה ה-19 היה ידוע שאם אנחנו מחממים גוף כלשהו, הוא פולט קרינה אלקטרומגנטית באורכי גל שונים. הקרינה הזאת שונה עבור כל אורך גל, והיא תלויה גם בטמפרטורה של הגוף (אבל לא בספקטרום הקרינה שהוא בולע). יש אורכי גל שנפלטים בעוצמה גדולה ואחרים בעוצמה נמוכה יותר, וכאמור כל הספקטרום הזה תלוי בטמפרטורה.
הנוסחה הסופית של קרינת גוף שחור הוצגה על ידי מקס פלנק בשנת 1900. לפניו הייתה נוסחת ריילי-ג'ינס שתיארה את הספקטרום לאורכי גל (שמסומנים באות למדא, λ) ארוכים, ונוסחת וין לאורכי גל קצרים. שתי אלו הן הכללות של מדידות לגבי אורכי גל מסוימים שתוארו על ידי נוסחאות מתמטיות מקורבות. הן התקבלו בתהליך של אינדוקציה, שלקחה אותנו מתוצאות פרטניות לגבי אורכי גל מסוימים, לנוסחאות כלליות יותר לכל אורכי הגל. מקס פלנק איחד את שתי הנוסחאות הללו ויצר את משוואת פלנק שנותנת לנו את הספקטרום לכל אורכי הגל. הגרף שמתאר את התוצאות האמפיריות של הקרינה באורכי הגל השונים (כל צבע הוא טמפרטורה שונה, במעלות קלווין) הוא הבא:
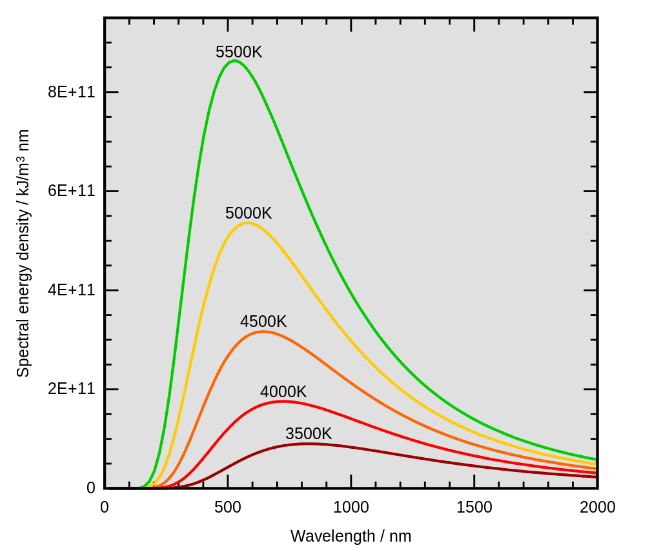
בשנת 1900 פלנק הציע נוסחה מתמטית שמתארת את הגרפים הללו, כאשר I זו האנרגיה שנפלטת מהגוף (בטמפרטורה T ואורך גל λ):
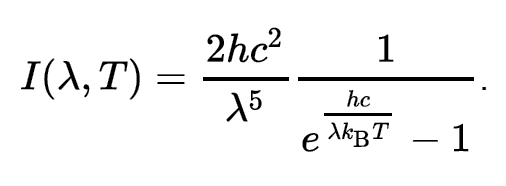
h – קבוע פלנק, T – טמפרטורה, – KBקבוע בולצמן, C – מהירות האור, λ – אורך הגל
כאן הסתיים תהליך האינדוקציה, שבו הגענו מתוצאות ספציפיות (לאורכי גל מסוימים) לתיאור מתמטי כללי (עבור כל אורכי הגל). אבל זו רק תחילת הסיפור, שכן אין לנו מושג מדוע באמת זוהי הנוסחה. זו רק הכללה של התוצאות האמפיריות ויצירת גרף ונוסחה כלליים. התהליך ממשיך בשנת 1905 (שנת הפלאות), כאשר איינשטיין מתבונן בנוסחה הזאת ומבין שהיא משקפת את העובדה שהאור מגיע במנות בדידות, פוטונים. מתוך כך הוא הסביר את האפקט הפוטואלקטרי, במאמר שהניח את היסודות לתורת הקוונטים. בשנת 1918 מקס פלנק עצמו הציג הסבר סטטיסטי מלא שמראה כי הנוסחה שלו משקפת התפלגות של קרינה של מנות בדידות (קוונטים) של אור בטמפרטורות שונות, כלומר הוא הראה שהנוסחה הזאת יכולה להיות מוסברת באמצעות תיאוריה קוונטית של האור.
זהו כבר צעד של אבדוקציה. מהתצפיות בקרינה של אורכי גל מסוימים הגענו לתיאוריה כללית (תורת הקוונטים וסטטיסטיקה קוונטית), שבמסגרתה ניתן לגזור את הנוסחה של פלנק (התוצר של האינדוקציה). הדרך המדעית הייתה כאן מהתצפיות בפרטים מסוימים לאינדוקציה (גרף ונוסחה), ומכאן לאבדוקציה (תיאוריה). שימו לב שהדרך של הגזירה הלוגית היא הפוכה: מהתיאוריה לנוסחה (הנוסחה נתנה לנו רמזים וכך הגענו לתיאוריה שחוזרת ומסבירה את הנוסחה), וממנה למקרים הפרטיים (אורך גל וטמפרטורה מסוימים). המסקנה היא שהכללה מדעית אינה סתם אינדוקציה. האינדוקציה נותנת לנו חוק פנומנולוגי כללי (תיאור של ההתנהגות), אבל ההבנה וההסבר המדעיים להתנהגות הזאת מגיעים רק עם היווצרות התיאוריה המדעית, כלומר באמצעות אבדוקציה. אינדוקציה נותנת לנו תיאור (כללי), אבדוקציה נותנת לנו הסבר.[6]
הפתעות מתמטיות
כאמור למעלה, יהודה שלח אליי מאמר מתמטי ובו מופיעה חידה מפתיעה מאד. כדי לחסוך לאלו מכם שלא מתמצאים, אתן דוגמה לא נכונה. נגדיר סכום ספרות סופי של מספר, שהוא התוצאה של סיכום של הספרות שלו, כך שאם יוצא עדיין מספר שאינו חד ספרתי מסכמים שוב את הספרות עד שמקבלים מספר חד ספרתי. כעת נניח שאנחנו בודקים את סכום הספרות הסופי של מספרים שונים, ומתברר לנו שאם מספר כלשהו מתחלק ב-9 סכום ספרותיו הסופי מתחלק גם הוא ב-9 (זו טענה נכונה כמובן). לדוגמה, אם נתבונן בסכום הספרות הסופי של 9, נקבל 9 כמובן. סכום הספרות הסופי של 18 הוא 1+8=9. סכום הספרות הסופי של 27 הוא 2+7=9. כך גם לגבי סכום הספרות הסופי של 36, 45 וכן הלאה. שימו לב שזה נכון גם למספרים גדולים מאד, כמו 1,089. סכום הספרות שלו הוא 1+0+8+9=18, וסכום הספרות של 18 נותן לנו את סכום הספרות הסופי, 9 כמובן. בואו נניח (זו הנקודה הלא נכונה בדוגמה), שהתכונה המעניינת הזאת מתקיימת עבור כל המספרים שמתחלקים ב-9 שבדקתם בזה אחר זה, אבל אם הייתה לכם מספיק סבלנות גיליתם פתאום שהיא לא מתקיימת עבור 676,026 (9X75,114. זהו המספר ה-75,114 בסדרה). האם זה יפתיע אתכם? אני חושב שכן. אם נניח שאחרי המספר הזה התכונה חוזרת להתקיים, אבל פתאום אנחנו מגלים עוד מספר ענק שבו היא שוב לא מתקיימת. המסקנה היא שהטענה הכללית (שסכום הספרות הסופי הוא תמיד 9) אינה נכונה, ולכן מדי פעם יש דוגמאות נגדיות. נראה קצת מוזר, אבל קורה, לא?
מה הייתם אומרים אם התכונה הזאת הייתה מפסיקה להתקיים החל מ-676,026 והלאה? כוונתי למצב שבו כל המספרים שמתחלקים ב-9 משם והלאה כבר לא מקיימים את התכונה הזאת. נדמה לי שזה היה יותר מפתיע מבחינתי. תכונה שמתקיימת באופן רציף לאורך הרבה מאד מספרים, אני מצפה שתמשיך להתקיים תמיד. אבל גם אם אני מגלה שהיא לא מתקיימת, אם זה קורה במספרים כאלה או אחרים שמפוזרים באופן מקרי על פני הציר, זה עוד איכשהו נסבל. אבל אם זה מפסיק להתקיים באופן מוחלט החל מנקודה מסוימת בסדרה, זה מאד מפתיע.
בשני המקרים הללו אני מניח שאדם סביר היה עושה אינדוקציה ומניח שהתכונה הזאת נכונה לכל המספרים בסדרה (כל המספרים שמתחלקים ב-9). אבל מדי פעם יכול להתברר לנו שהאינדוקציות שלנו שגויות. מבין שתי ההפתעות שתיארתי, קשה לי להסביר מדוע השנייה מפתיעה אותי יותר מהראשונה. העובדה שיש טענה שנכונה להרבה מספרים אבל לא לכולם, אינה בעייתית כשלעצמה. ואם היא אינה נכונה, אין שום סיבה להניח שאי הנכונות שלה תופיע מיד במספר הראשון, או במספר ה-58 בסדרה. אין מניעה עקרונית שזה יופיע במספר ה-75,114 בסדרה. מסיבה זאת התופעה הראשונה נראית לי פחות מפתיעה. אבל אם משהו מתקיים לאורך הרבה מספרים, וממספר מסוים והלאה זה מפסיק לגמרי להתקיים, זה כבר מפתיע יותר.[7]
בחזרה לדוגמה שקיבלתי
במאמר הנ"ל מתוארת תופעה דומה מאד למה שתיארתי כאן (אבל שם זו תופעה אמתית). התבוננו בסדרת אינטגרלי Borwein הבאה (שמה ניתן לה על שם שני פיזיקאים, אב ובנו, שגילו אותה):

מתברר שכל אחד מהם עד השביעי (I1…I7) נותן בדיוק אותה תוצאה עגולה ויפה להפליא: 1.[8] אבל באינטגרל השמיני (I8) מופיעה כבר סטייה קטנה (עשר ספרות אחרי הנקודה), והתוצאה כבר מעט קטנה מ-1. משם והלאה (I9 והלאה) המצב מתדרדר יותר ויותר למטה. אם אני מבין נכון (לאור ההסבר שניתן שם לתופעה), דומני שבסוף זה ממש מגיע ל-0.
התופעה הזאת ממש מפתיעה מבחינתי (וכנראה גם מבחינת רבים נוספים, אחרת המאמר לא היה נכתב). מה גורם לסדרה שמוגדרת בצורה מונוטונית והדרגתית להיקטע באחת בצורה כזאת? היינו מצפים שהתוצאות ימשיכו ויהיו 1 לכל אורך הדרך (באינדוקציה מהמקרים הראשונים). שימו לב שזוהי הפתעה מהסוג השני ולא הראשון, כלומר מהזן המפתיע יותר. אגב, כפי שתראו מיד, באותה צורה אפשר לארגן סדרות כאלה שייקטעו החל מ-75,114 Iאו כל איבר אחר שתרצו.
החלק הגאוני בעניין (זו רק סקירה. ההסבר במקור הוצג על ידי שני פיזיקאים אחרים במאמר משנת 2019) הוא ההסבר שהוצע לתופעה המפתיעה הזאת. בלי להיכנס לפרטים מתמטיים, טענתם הייתה שכל אינטגרל כזה מציג גודל שמתואר על ידי הילוך אקראי כפי שאתאר כעת. הניחו שיש אוסף נקודות שמפוזרות באופן אחיד על פני כל ציר X. כל אחת מהן מתקדמת ימינה או שמאלה על הציר כאשר גודל כל צעד מתפלג בשווה על קטע באורך נתון כלשהו, נאמר בקטע (Δ,Δ-). ברור שאחרי הצעד הראשון לא ישתנה שום דבר בהתפלגות הכללית (כי יש סימטריה מלאה בין כל הנקודות על הציר). כך גם אחרי כל צעד בהמשך. אם נגדיר את התוצאה כגובה ההתפלגות בנקודה X=0 אחרי הצעד ה-n, אזי אם גובה ההתפלגות בהתחלה הוא 1, התוצאה תהיה 1 אחרי כל מספר צעדים בכל נקודה על הציר ובפרט בנקודה X=0.
אבל מה יקרה אם ההתפלגות ההתחלתית אינה פרוסה על פני כל הציר אלא רק על פני הקטע (1,1-). אזכיר שאנחנו מסתכלים על גובה ההתפלגות בנקודה X=0 אחרי הצעד ה-n. נניח שבצעד הראשון כל הנקודות צועדות ימינה או שמאלה כשאורך הצעד המקסימלי הוא Δ=1/3, ובצעד הבא אורך הצעד המקסימלי הוא Δ=1/5, וכך הלאה עם המספרים האיזוגיים במכנה. הכותבים הסבירו שהאינטגרל I1 מתאר את כמות הנקודות ב-X=0 אחרי הצעד הראשון. האינטגרל I2 מתאר את מספר הנקודות אחרי הצעד השני, וכן הלאה. חשבו מה אמור להתקבל במצב כזה. בצעד הראשון, הנקודה X=0 'חושבת' שהיא חיה בתוך התפלגות אינסופית. הצועדים שנכנסים אליה או יוצאים ממנה הם רק מהנקודות שקרובות אליה, שכן היא יכולה להיות מושפעת רק מהקטע שמרוחק ממנה לכל היותר 1/3 לכל כיוון. בתוך הקטע הזה בקרבתה הכל נראה מפולג אחיד, ולכן התוצאה שמתקבלת היא בדיוק כמו בבעיה שעוסקת בהתפלגות ראשונית שפרוסה על פני כל הציר. לכן ברור שהתוצאה, כלומר מספר הנקודות שנמצאות ב-X=0 היא 1, כמו במקרה האינסופי. אחרי הצעד השני היא כבר יכולה להתחיל להרגיש את הצועדים שנמצאים במרחק מקסימלי של 1/3 + 1/5 ממנה לשני הצדדים. מכיוון שהמרחק הזה עדיין קטן מ-1, אזי עדיין מבחינת המקום X=0 התוצאה היא כמו התפלגות התחלתית אינסופית. לכן גם במצב זה התוצאה היא עדיין 1. כך גם לגבי הצעד השלישי והרביעי. מתי הנקודה X=0 תוכל כבר להרגיש את העובדה שהפילוג הראשוני אינו אינסופי? כאשר מתחילה להגיע אליה השפעה מנקודות שנמצאות מעבר לקטע של הפילוג הראשוני (כלומר מנקודות על הציר שנמצאות ימינה ל-X=1 או שמאלה ל-X=1-). כשאלו מתחילות להגיע אליה, היא פתאום "מבינה" שהפילוג סביבה אינו אינסופי, ואז מתחילה סטייה מהתוצאה הקבועה. ברור שהתוצאה תתחיל לרדת, שכן ההתפלגות שהייתה מרוכזת בהתחלה בקטע מסוים מתחילה להתפרס על פני כל הציר. מתוך ההסבר שהצעתי תוכלו להבין שזה קורה בדיוק באינטגרל I8, שכן אחרי הצעד השביעי מתחילים להגיע לנקודה X=0 השפעות מהמרחק שעובר את 1. הסיבה לכך היא שהסדרה הבאה: …1/3+1/5+1/7+1/9+1/11+1/13+1/15 עוברת את 1 אחרי שמונה איברים. לכן התוצאה מתחילה להיות מעט קטנה מ-1, כי חלק מהצועדים בורח החוצה אל מחוץ להתפלגות הראשונית (ל-X-ים שנמצאים מימין ל-1 או משמאל ל-1-), ולכן הגובה של ההתפלגות מתחיל לרדת. אחרי מספיק צעדים, כלומר אינטגרלים בהמשך הסדרה הזאת יילכו ויתקרבו ל-0 (כי בסוף ההתפלגות הראשונית נוטה להתפרס בשווה על פני כל הציר).
זהו ההסבר שהם הציעו לתופעה המפתיעה שתיארתי. זו הסיבה שתוצאת האינטגרלים הללו מתחילה להשתנות החל מהאיבר השמיני. אגב, מכאן קל מאד לבנות סדרות אינטגרלים שיתחילו את הסטייה מהאיבר ה-75,114, או כל איבר אחר שתרצו. פשוט בנו סדרת צעדים שסכומה יעבור את 1 אחרי 75,114 איברים. זה ממש לא קשה.
האם זו אבדוקציה? בין מדע למתמטיקה
כאמור, יהודה שלח לי את המאמר הזה כדוגמה לאינדוקציה שנעשית בלי אבדוקציה ברקע. מי שיתבונן בסדרה של שבעת האינטגרלים הראשונים ייטה לחשוב באינדוקציה שכל האינטגרלים בהמשך ייתנו גם הם את התוצאה 1. אבל הוא יטעה. ההסבר שהצגתי כאן מסביר מדוע לא נכון להמשיך את הסדרה באינדוקציה טבעית ופשוטה. לכאורה זה בדיוק כמו האבדוקציה שמסבירה מדוע המשך הסדרה שלמעלה יכול להיות 11 ולא 9, או שתוצאת הקו"ח אינה 1 גם אם בגלל פירכת שורה עוברים מטיעון השורות לטיעון העמודות וכן הלאה. כשמבינים את ההסבר התיאורטי, יכולים לגלות שהאינדוקציה שלנו לא נכונה.
אבל כפי שעניתי ליהודה אחרי קריאת המאמר, לדעתי זו אינה דוגמה לאבדוקציה. ההסבר שניתן כאן הוא מטיפוס אחר. אבדוקציה מציעה תיאוריה כללית, שהנוסחה יכולה להיגזר ממנה, וכל המקרים הפרטיים מוסברים במסגרתה. ואילו כאן ההסבר שהוצע לא מציג חוק כללי אלא תופעה ספציפית שמתוארת על ידי הנוסחה הזאת. הנוסחה הזאת יכולה לתאר גם תופעות אחרות ולא הילוך מקרי, ועדיין התוצאה הזאת תהיה נכונה. ההילוך המקרי הוא דוגמה פרטית ולא חוק כללי, והדוגמה לא מסבירה את הנוסחה באופן דדוקטיבי-נומולוגי אלא מדגימה אותה על מקרה פרטי.
במתמטיקה מכנים זאת שההילוך המקרי מהווה 'מודל' לתיאוריה של האינטגרלים הללו. זהו מקרה שמתואר על ידי הנוסחאות המתמטיות. כמו שחשבון וקטורי הוא תיאוריה מתמטית כללית, ויש הרבה מאד תופעות בפיזיקה שמהוות מודל אליו. כוחות, מהירויות, תאוצות, מומנטים, כל אלו הם גדלים שמתוארים על ידי החשבון הווקטורי, ולכן הם מהווים מודל לתורה הווקטורית. ההילוך המקרי הוא מודל לתיאוריה שמתוארת על ידי האינטגרלים הללו (ובהחלט יכולים להיות עוד מודלים רבים אחרים אליו).
ככלל, דומני שאבדוקציה היא הליך ששייך באופן מהותי למדע ולא למתמטיקה. מתמטיקה לא עוסקת בהיסקים של אנלוגיה ואינדוקציה אלא אך ורק בדדוקציה, כלומר בהיסקים הכרחיים מהכלל אל הפרט. המדע עוסק באנלוגיה ואינדוקציה, ולכן גם באבדוקציות (שהן סוג של אינדוקציות).
[1] האינטואיציוניסטים אמנם חולקים על כך, אבל זהו רק פלפול פילוסופי.
[2] בלשונו של פילוסוף המדע קרל המפל, זוהי הסכימה הדדוקטיבית-נומולוגית, שבמסגרתה החוק הכללי מהווה הסבר למקרים הפרטיים אם ניתן לגזור אותם ממנו בדדוקציה.
[4] ראו בספרי אמת ולא יציב, פרק עשרים.
[5] יש שני יוצאי דופן, בב"ק ובנידה, ובשניהם הטבלה אינה סימטרית. לא ניכנס לזה כאן.
[6] שהוא תמיד מטיפוס 'העמדה על הלא מוכר' (ראו נספח ב לספרי אלוהים משחק בקוביות וכאן).
[7] תחושתי היא שזה קשור להבחנה בין אנדרפיטינג ואוברפיטינג, שתוארה בטור 243.
[8] לצורך הנוחיות אני מחלק כל אינטגרל ב-π.
לגלות עוד מהאתר הרב מיכאל אברהם
Subscribe to get the latest posts sent to your email.


[סיבוב ק"ו. אי הוא גם חומרא בשן (פירכא לטיעון השורות) וגם מקום חדש שחהנ יכול להיות בדיוק כמוהו (פירכא לטיעון העמודות). לכן לעניין קושייתך הכללית על סיבובי ק"ו גם במקום שהפירכא היא מדין נתון לי זכור אחרת כדבר ידוע ואולי אני שוגה בפשוטות. אם אומרים "מה שן שפטורה ברהר חייבת בחהנ, קרן שחייבת ברהר אינו דין שחייבת בחהנ. פירכא מה לשן שחייבת באי תאמר בקרן שפטורה באי" אז אה"נ אפשר גם "מה רהר ששן פטורה בה קרן חייבת בה, חהנ ששן חייבת אינו דין שקרן חייבת בה. פירכא אי יוכיח ששן חייבת בו וקרן פטורה בו". לא כך?
רק אם הפירכא היא מסברא ולא מדין ידוע כגון על טיעון השורות פירכא מה לקרן שמטילה אימה ברהר ולכן חייבו בה כי היכי דלינטריה אבל בחהנ קרן פטורה, אז אם מסובבים לטיעון עמודות וטוענים שחהנ חמורה מרהר אז הפירכא הזאת מסברא היא אולי לא רלוונטית (אם כי גם כאן אפ"ל שהפירכא לעולם עומדת). ומ"מ במקום שאפשר לסובב אז לכל הפחות תוספות אמורים לטפל בזה וכמדומה שהם אכן עושים את זה ואם לא הם אז העצמות יוסף בקידושין. ]
הפכתי בטעות את משמעות המונחים טיעון שורות וטיעון עמודות (בטור טיעון שורות משתמש בשורות כדי למצוא היררכיה בין העמודות. אני בטעות השתמשתי בלשון טיעון שורות עבור הטיעון שמוצא היררכיה בין השורות).
לא מצליח לעקוב. אתה מדבר על הבלעת פירכא?
לא התכוונתי להבלעת פירכא (במונחים שאני מכיר להבלעת פירכא, אולי אני לא מדייק). פתחת בקושיא למה הגמרא אחרי פירכא כמעט תמיד לא מסובבת את הקל וחומר. ואז הסברת את העניין בצורה נפלאה ככתוב בספר הראשון. הקושיא לא ברורה לי (וממה שזכור לי התייחסו אליה במפורש). עוד לפני ההסבר הנפלא, איך סיבוב קל וחומר יכול להבריח מפני הפירכא?
כתבת שאם יש ק"ו של נושאים: "שן שפטורה ברשות הרבים חייבת בחצר הניזק, קרן שחייבת ברשות הרבים אינו דין שחייבת בחצר הניזק" ואז פירכא "מה לשן שכן חייבת באי בלב ים, תאמר בקרן שפטורה באי בלב ים", אז אפשר לסובב את הקל וחומר לקל וחומר של מקומות "מה רשות הרבים ששן פטורה בה קרן חייבת בה, חצר הניזק ששן חייבת בה אינו דין שקרן חייבת בה". עד כאן דבריך בשלב הקושיא.
למה אי אפשר לפרוך "אי בלב ים יוכיח, ששן חייבת בו וקרן פטורה בו". [מובן שביסוד כל הדברים עומד ההסבר שלך, אבל למה הוא נחוץ כדי כדי לפתור את הקושיה הבסיסית הזאת].
זו כשלעצמה אינה בהכרח פירכא. זה שההיררכיה לא קיימת ביחס לנושא שלישי (בין עמודה ראשונה לשלישית) אינו פורך את ההיררכיה המאונכת כשלעצמה (בין עמודה ראשונה לשנייה). אמנם אחרי שרואים את הניתוח במונחי פרמטרים (אלפא) אכן מתברר שזו כנראה פירכא.
באינדוקציה הדגש על התולדה, ובאבדוקציה על הכלל או המקור.
3, 5, 7, 9,
מה המספר הבא בסדרה? באינדוקציה פשוטה – 11. אולם אם אלו מספרים בהפרש 1 מחזקות של המספר 2, המספר הבא בסדרה 15.
3, 5, 7, 11,
מה המספר הבא בסדרה? באבדוקציה פשוטה 13. אולם אם אלו מספרים שההפרש ביניהם עולה בהדרגה, המסר הבא בסדרה 15.
עתה:
3, 5, 7, ?, 15
מה המספר החסר בסדרה?
13, אם הסדרה הכללית היא 3, 5, 7, 13, 15, 17, 23, 25, 27…
לא בכדי החכמים הקדמונים נחלקו האם אין בפרט אלא מה שיש בכלל, או שמא כלל אינו אלא אוסף של פרטים.
"ההילוך המקרי הוא דוגמה פרטית ולא חוק כללי". הטענה מובנת ואכן יש הבדל. אבל האם לא נכון לומר שכל המודלים של נוסחא הם איזומורפיים זה לזה? ואם אכן עבור כל שני מודלים קיים איזומורפיזם כזה אז מה כעת משמעות ההבדל בין דוגמה פרטית לחוק כללי. [אגב במקרה ממש לא מזמן הסדרה הזו הוצגה בערוץ הקסום הזה https://did.li/borwein%5D.
השתבש הלינק הודות לסוגר המרובע
https://did.li/borwein
הם אכן איזומורפיים, אבל ההסבר אינו עצם קיומו של המודל אלא ההבנה שנוצרת מהסתכלות במודל. ההבנה הזאת אינה הסבר כללי, אלא הבנה מתוך מודל אחד.
דומני שהתער של אוקאם הוא ההסבר לרבות מהדוגמות שהבאת, לדוגמה, מדוע ההמשך הטבעי ל3, 5, 7 הוא 9 ולא 11, וכן מדוע זה מפתיע שתכונה כלשהי שנכונה למאות רבות של מספרים, מפסיקה להתקיים ממספר מסויים ואילך. אגב, לכל מספר יש תכונה שמפסיקה להתקיים בדיוק אצלו, דהיינו שהוא גדול מהמספרים שקטנים ממנו. מדוע זה לא מפתיע? שוב מפני שהסיבוכיות בתיאור הכלל הזה שווה לסיבוכיות של המספר עצמו, מה שאין כן בדוגמה המפתיעה בכתבה כאן.
לא הבנתי מה הקשר לתער של אוקאם.
התכונות הטריוויאליות הללו כמובן לא מפתיעות אף אחד ולכן אינן מעניינות.
השאלה היא כיצד מכמתים את מידת הטריוויאליות של תכונה. ישנו תחום ביסודות הלמידה האלגוריתמית שהוא פורמליזציה של תער אוקאם שעונה על כך: https://en.wikipedia.org/wiki/Minimum_description_length
בדוגמה של השלמת הסדרה, בנהתן רצף סופי של איברים, פולינום מדרגה השווה לאורך הסדרה מספיק כדי לתאר אותה, וממילא לקבוע את האיברים הבאים. זה ידוע שקביעת הסתברות למאורע קובע את אורך התיאור הנצרך לאינסטנציה שלה (ע״י בניית קידוד אריתמטי, לדוגמה). כאן, לדוגמה, בנסיבות, יהיה סביר לקבוע את ההתפלגות הגיאומטרית הן לדרגת הפולינום, והן למקדמים שלו (בהנחה והם שלמים). יש לשים לב שלא מדובר בשערוך של ההתפלגות כגיאומטרית, אלא כהחלטה להשתמש בהתפלגות ליצירת קוד.
תער אוקאם הוא הבסיס כמעט לכל הטור שכתבת, אבל המקרה הזה הוא דוגמה ישירה מאד לעקרון התיאור הקצר לעיל.
כנ״ל לאמירתך ״התכונות הטריוויאליות הללו כמובן לא מפתיעות אף אחד, ולכן אינן מעניינות״ – הן טריוויאליות, מפני שהן לא מקודדות בצורה יעילה יותר שום דבר. עקרון התיאור הקצר מכמת אובייקטיבית את זה שזהו טריוויאלי.
במקרים מסובכים יותר, זהו עקרון מבוסס תיאורטית כדי לקבוע היפרפרמטרים ללמידה לא מבוקרת: https://scholar.google.co.uk/scholar_url?url=https://citeseerx.ist.psu.edu/document%3Frepid%3Drep1%26type%3Dpdf%26doi%3Dc6e7e4bdf941322b03e7abe871af66119bde3c0f&hl=en&sa=X&ei=lknKY-z7O4jQmAGhnojwCg&scisig=AAGBfm3BOJoWms-exURNRBOE3hdWRDNhcQ&oi=scholarr
דומני שאתה מתכוון למה שהערתי בהערה 7. אבל אני חוזר ואומר שאתה מציע תיאור מדוע משהו מפתיע יותר מאחרים (אוברפיטינג מול אנדרפיטינג), אבל כאן לא עסקתי בזה (למעט הקטע שדן בהשוואה בין שני סוגי ההפתעה). עסקתי בכך שלפעמים קורים גם דברים מפתיעים, בלי קשר לשאלה מדוע הם מפתיעים. ודאי תודה שבסדרת האינטגרלים הללו יש משהו מאד מפתיע לפי הקריטריונים שהזכרת. זה מה שחשוב לדיון שלי. השאלה למה זה מפתיע ועד כמה, היא שאלה אחרת.
ההפנייה לוויקיפדיה של נוסחת ויין אינה נכונה . היא הפנייה לחוק ההסחה של ויין שגם קשור להתפלגות הקרינה של גוף שחור אבל הוא משהוא אחר מנוסחת וויין ( שגם קרויה "חוק ההתפלגות של וויין " ) שאותה מכלילה נוסחת פלאנק :.זו ההפניה הנכונה –
https://en.wikipedia.org/wiki/Wien_approximation
תודה.
גם ההסבר ההיסטורי לנוסחת פלאנק לא מדויק. כבר פלאנק עצמו בפיתוח הנוסחה הניח שהאנרגיה של הקרינה נפלטת במנות בדידות. הוא לא ידע להסביר למה ( והניח שזה קשור איכשהוא לכך שהחומר עצמו שפולט את הקרינה ( החומר של הגוף השחור) בנוי באופן בדיד. כלומר ממולקולות שהן אלו שפולטות את הקרינה). איינשטיין השתמש בתוצאה הזו בשביל להסביר את האפקט הפוטואלקטרי מתוך הבנה שזה האור עצמו שבדיד (בנוי מחלקיקים) וזו הסיבה לכך שהאנרגיה שלו נפלטת במנות בדידות מהגוף השחור (אבל שזה לא קשור לכך שהחומר בנוי ממולקולות)
הנה : https://he.wikipedia.org/wiki/%D7%9E%D7%A7%D7%A1_%D7%A4%D7%9C%D7%90%D7%A0%D7%A7
כפי שכתוב בהפנייה פה ב1918 הוא רק זכה על כך בפרס נובל. למרות שהרבה ערערו על כך וטענו שבעצם עיקר הגילוי הוא של אלברט איינשטיין . היחס ביניהם מזכיר לי את היחס שבין קולומבוס ( פלאנק) שהגיע ראשון לאמריקה וחשב שהגיע להודו , לאמריגו וספוצ'י שהגיע אחריו והבין שמדובר ביבשת חדשה ( איינשטיין) ועל שמו היא נקראת אמריקה. אז קולומבוס "גילה" את אמריקה.