משמעותן ההלכתית של מכפלות הסתברותיות: ג. הסתברות מותנה ורוב שאיתרע (טור 614)

בס"ד

בשני הטורים האחרונים עסקתי במכפלות הסתברותיות. בטור האחרון עמדתי על חשיבותה של התלות בין אירועים לעניין חישוב ההסתברות המשותפת שלהם. נושא זה עלה כאן לא פעם (חפשו 'נוסחת ההסתברות השלימה', או 'נוסחת בייס'). ברוב ככל הטורים הנ"ל עסקתי בבלבול בין שתי הסתברויות מותנות: P(A/B)  ו-P(B/A). כאן חשבתי לנצל את ההזדמנות ולבחון כמה דוגמאות שבהן מבלבלים בין ההסתברות המוחלטת P(A) להסתברות המותנה[1] P(A/B). בסופו של חשבון נראה שגם כאן נכנסת ההנחה שנדונה גם בשני הטורים הקודמים, שברוב המקרים הרוב ההלכתי הוא רוב נגטיבי ולא פוזיטיבי. אנחנו גם נראה שהכלים שבהם יש להשתמש כאן (הסתברות מותנה, מכפלת הסתברויות, עץ אפשרויות) דומים לאלו ששימשו אותנו בטורים הקודמים. כאן גם נראה ייצוג ויזואלי של התופעה הזאת.

תזכורת: הסתברות מותנה

הסתברות של אירוע כלשהו קובעת מה הסיכוי שהוא יתקיים. ניתן לקבוע הסתברות כזאת כשיש לנו מרחב מאורעות והתפלגות. למשל, בהטלת קובייה, מרחב המאורעות כולל שישה אירועים, שהם שש התוצאות האפשריות של ההטלה. ההתפלגות תלויה בשאלה האם הקובייה הוגנת או לא. בקובייה הוגנת הסיכוי לכל אחד מהמאורעות שווה, ומכיוון שתמיד הסיכויים לכלל האירועים מסתכמים ל-1, לכן הסיכוי לכל אחד מהם הוא 1/6. ומכאן שאם אשאל מה הסיכוי לקבל בהטלת קובייה הוגנת 5, התשובה תהיה 1/6.

אבל ניתן לשאול מה הסיכוי לקבל 5 כאשר יש לנו מידע נוסף כלשהו, למשל אם ידוע שהתוצאה היא אי זוגית? כאן התשובה תהיה 1/3 (כי יש שלוש תוצאות אי זוגיות וכולן שוות הסתברות). אם ידוע שהתוצאה הייתה זוגית הסיכוי הוא כמובן 0 (כי 5 אינו זוגי). משמעות הדבר היא שהאירוע 5 תלוי באירוע 'תוצאה אי זוגית' או 'תוצאה זוגית'. הם לא בלתי תלויים.

אנחנו מסמנים את הגדלים הללו כך:

הסיכוי לאירוע A הוא P(A). הסיכוי לאירוע B הוא P(B). הסיכוי לאירוע A אם ידוע שקרה B, הוא P(A/B). נניח שהאירוע A הוא התוצאה 5, והאירוע B הוא תוצאה אי זוגית, אזי מתקבל: P(A) = 1/6, P(B) = 1/2 וכמובן P(A/B) = 1/3. במקרה זה מקבלים שההסתברות המלאה P(A) היא מכפלת ההסתברויות P(A/B)*P(B). אבל זה לא תמיד המצב. כדי להבין זאת, התכוננו באירוע C, שהוא: התקבלה תוצאה זוגית. הסתברותו היא P(C)=1/2, ואפשר גם לראות אותו כסיכוי של האירוע המשלים ל-B (כלומר B~). מכאן תוכלו לראות שמתקיים גם: 0=P(A/~B).

הסתברות מותנה בתוך עץ אפשרויות

אתם יכולים לראות שהסיכוי שיצא 5 ניתן לתיאור באמצעות עץ אפשרויות כפי שראינו בשני הטורים הקודמים:

הסיכוי לקבל 5 מורכב משתי אפשרויות (הקצה השמאלי ביותר והשני מימין):

• בענף הימני כדי שייצא 5 צריך לעבור הטלה אי זוגית (סיכוי 1/2) ואז יש הסתברות מותנה של 1/3 לקבל 5. לכן הסיכוי ל-5 הוא 1/6 (מכפלת הסיכויים על המסלול הימני: 1/2*1/3=1/6).
• בענף השמאלי קודם יוצאת תוצאה זוגית (סיכוי 1/2) ואז ההסתברות המותנה לקבל 5 היא 0. לכן הסיכוי לקבל 5 על המסלול הזה הוא 0 (מכפלה של הסיכויים על המסלול השמאלי: 1/2*0=0).

בכל מסלול כזה, האירוע הראשון מצוי בחלק העליון של העץ, ומה שקורה אחריו צריך להילקח בחשבון כהסתברות מותנה. מה הסיכוי שהתוצאה זוגית או אי זוגית. ואת זה לכפול בסיכוי המותנה שיצא 5 בהינתן שהתוצאה היא אי זוגית או זוגית. הסיכוי המוחלט  לקבל 5 מורכב משתי האפשרויות הללו. ובצורה כללית יותר ניתן לכתוב כאן את נוסחת ההסתברות השלימה:

P(A) = P(A/B)*P(B) + P(A/~B)*P(~B)

נוסחה זו מתארת את ההסתברות המוחלטת לקבל 5 כסכום של שתי אפשרויות. המכפלה שראינו למעלה נובעת מכך שבמקרה זה המחובר השני הוא 0. זה לא תמיד המצב.

צורה אחרת לתאר את המכניזם של תלות סטטיסטית הוא דרך צמצום של מרחב המאורעות. תוצאה זוגית או אי זוגית מצמצמת את מרחב המאורעות הרלוונטי (אלו שיכולות לקרות), ולכן משתנה גם הסיכוי של המאורע שבו אנחנו עוסקים. ניתן לתאר זאת בשרטוט כך:

המרחב הוא האליפסה כולה, והיא מכילה 6 מאורעות. אם אני מתייחס לכל המרחב הסיכוי לקבל 5 הוא 1/6. אבל כאשר ידוע לי שהתוצאה היא אי זוגית אני בעצם מצמצם את המרחב על ידי קו הגבול הדק שבשרטוט, כך שאנחנו מצויים בחלק האליפסה שמשמאלו. בה במידה, תוצאה זוגית מצמצמת אותנו לחלק הימני של האליפסה. ברגע שהמרחב שלנו הצטמצם, הוא מכיל פחות מאורעות, ואז ברור שהסיכוי למאורע שמעניין אותנו (5) משתנה. בצד שמאל הוא 1/3 (גדול מאשר במרחב כולו) ובצד ימין הוא 0 (קטן יותר מאשר במרחב כולו). הסיכוי לקבל 5 בצד הימני או השמאלי הוא הסתברות מותנה. לדוגמה: בהינתן שאני מצמצם את הדיון לצד השמאלי מה הסיכוי לקבל 5? 1/3. נוסחת ההסתברות השלימה אומרת לי שהסיכוי לקבל 5 הוא או להימצא מימין (סיכוי 1/2) – שאז הסיכוי המותנה הוא 0, או להימצא משמאל (סיכוי 1/2) – ואז הסיכוי המותנה הוא 1/3. לכן את הסיכוי המוחלט 1/6 ניתן להציג כסכום של שתי מכפלות שכל אחת מייצגת אפשרות של לבחור באחד הצדדים, כפי שראינו למעלה.

כמובן שניתן היה גם לחלק את המרחב בצורות אחרות. למשל, כשהאירוע B הוא שהתוצאה גדולה או שווה ל-5,. או שהתוצאה מתחלקת ב-4 וכדומה. כל חלוקה כזאת תניב הסתברויות מותנות שונות בשני צדדיה, אבל הסיכוי המוחלט תמיד יהיה סכום המכפלות של האפשרויות השונות, ושם תמיד נקבל 1/6.

דוגמה: "חזקה מה שתחת יד האדם הוא שלו"

ההלכה קובעת שאם מתנהלת התדיינות בין שני בעלי דין, נטל הראיה מוטל על התובע: המוציא מחברו עליו הראיה. הגמרא בב"ק מו ע"ב דנה במקורו של הכלל הזה:

א"ר שמואל בר נחמני מניין להמוציא מחבירו עליו הראיה שנאמר מי בעל דברים יגש אליהם יגיש ראיה אליהם מתקיף לה רב אשי הא למה לי קרא סברא הוא דכאיב ליה כאיבא אזיל לבי אסיא.

בהתחלה מובא לכך פסוק, אבל לבסוף זה נדחה מפני שניתן ללמוד זאת מסברה: מי שכואב לו יילך לרופא. בפשטות זו טענה משפטית ולא הסתברותית: התובע רוצה שבי"ד יפעל, כלומר יוציא ממון מהנתבע וייתן לו. לעומת זאת, הנתבע לא רוצה מביה"ד מאומה (הוא רוצה שבי"ד לא יעשה כלום והכסף יישאר אצלו). לכן נטל הראיה הוא על התובע: אם אתה רוצה שבי"ד יפעל עליך לספק לו סיבה טובה לעשות זאת. בהיעדר סיבה בי"ד לא יפעל. זהו יתרון שניתן ל'מוחזק' על פני התובע. בכל אופן, בין אם מדובר בפסוק ובין אם מדובר בסברה, נראה שהכלל הזה אינו משקף אומדנא עובדתית (שבאמת סביר יותר שהנתבע צודק), אלא כלל משפטי.

לא פעם עולה טענה (ראו למשל באנצי"ת ע' חזקת מטלטלים') שבעצם מאחורי הסברה והפסוק מונח עיקרון הסתברותי, שמבוסס על הכלל: "חזקה כל מה שתחת יד האדם שלו".  הניסוח הזה לא מופיע בתלמוד עצמו והוא מצוי רק בראשונים, אבל רבים מזהים אותו עם הכלל 'המוציא מחברו עליו הראיה', כלומר עם מושג המוחזקות (ראו סקירה כאן). אלא שהזיהוי הזה הוא בעייתי: אם באמת מדובר בחזקה הסתברותית, מדוע נדרש פסוק ולמה הגמרא לא הציגה את הסברה הזאת אלא סברה משפטית? יתר על כן, הסברה המשפטית מותירה את העניין בספק ולא מכריעה מי צודק, עד כדי כך שעולה דיון באחרונים האם מי שזכה בממון מכוח מוחזקות נחשב ממש כבעליו לכל דבר ועניין. אבל אם העיקרון הזה מבוסס על ראיה הסתברותית, כלומר על החזקה מה שתחת יד האדם הוא שלו, אזי יש כאן ראיה פוזיטיבית לטובת הנתבע. אם כך, לכאורה הספק הזה לא מתעורר.

ניתן לחלק בין תביעת כסף לתביעה על חפץ מסוים. כשמישהו תובע ממני כסף שלוויתי או תשלומי נזק ואני מכחיש, אין כאן חפץ מסוים שניטש לגביו ויכוח. לכן כאן קשה לדבר על יתרון לטענתו של מי שמחזיק בכסף. הלווה/המזיק אמנם מוחזק בכסף, אבל קשה לגזור מכאן שהכסף כנראה שלו (כלומר שהוא לא לווה או לא הזיק). החזקה הזאת נכונה לגבי חפצים. אם תהיה תביעת בעלות על חפץ כלשהו, שם לכאורה יכולה לעלות החזקה הזאת ולהכריע את הדיון. אם כן, במחלוקת על כסף נראה שקשה ליישם את החזקה הזאת. אבל האם לגבי חפצים באמת אין צורך בסברה או בפסוק?

הסבר: הסתברות מותנה

התשובה לכך היא שלילית. כדי להבין זאת, עלינו לחזור לשאלה ההסתברותית. כאשר נעשה סקר של כלל החפצים בעולם נגלה שרובם נמצאים אצל בעליהם. כלומר בהינתן חפץ A בפנינו, ההסתברות שמי שמחזיק בו הוא בעליו גדולה מההסתברות שמישהו אחר הוא בעליו. לכאורה זו ראיה לטובת המחזיק בחפץ. אלא שהשיקול הזה נכון רק אם נבחר באופן מקרי חפץ כלשהו בעולם. אבל במקרה של התדיינות בבית דין בין שני בע"ד לגבי הבעלות על החפץ הזה, מדובר בחפץ שניטשת לגביו מחלוקת. בתת הקבוצה של החפצים שלגביהם ניטשת מחלוקת משפטית, איני רואה סיבה להניח שברוב המקרים הנתבע (המוחזק) צודק. האם יש יסוד להניח שתובעים משקרים יותר מאשר נתבעים (מתגוננים)? להיפך, ישנה חזקה "שאין אדם תובע אלא אם כן יש לו עליו" (ראו שבועות מ ע"ב), שנותנת יתרון להנחה שהתובע אינו משקר.

שורשו של הכשל הוא שוב במושגים של הסתברות מותנה. נניח שאנחנו דנים בבעלות על חפץ מסוים. ההסתברות שהוא שייך ל-A שמחזיק בו היא P(A), ולצורך הדיון היא שווה למספר החפצים שנמצאים ברשות בעליהם חלקי מספר החפצים הכללי בעולם. אם יש בעולם מיליון חפצים, ההנחה היא שרובם הגדול, נניח 850,000 מהם, מונחים אצל בעליהם. לכן הסיכוי שהחפץ שבפנינו נמצא אצל בעליו הוא: P(A) = 0.85. אבל את החפץ המדובר לא בחרתי באופן מקרי מכלל החפצים בעולם. הוא חלק מתת קבוצה מיוחדת של חפצים שלגביהם ניטש ויכוח. בתת הקבוצה הזאת יכולה להיות התפלגות שונה לגמרי בין חפצים ששייכים לתובע ולנתבע, כלומר הסיכוי שמי שמחזיק בחפץ הוא בעליו כבר לא בהכרח 0.85. וכאמור, סביר מאד שההתפלגות כאן שונה (אפריורי נראה שהסיכוי של שניהם בערך שווה).

במונחי הסתברות מותנה, עצם העובדה שמדובר בחפץ שנמצא במחלוקת, מצמצמת אותנו מקבוצת כלל החפצים בעולם לקבוצת החפצים שבמחלוקת. בפשטות התמונה דומה מאד לאליפסה שראינו למעלה:

מתוך 18 חפצים יש 4 שבמחלוקת (אלו המושחרים). אם היינו עושים את הסטטיסטיקה על כלל האליפסה, היינו מקבלים: P(A) = 0.85. אם היינו עושים את הסטטיסטיקה על חלק כלשהו ממנה, כמו למשל על הצד השמאלי של קו הגבול שמסומן שם, היינו מקבלים תוצאה אחרת כלשהי. ואם נעשה סטטיסטיקה על ארבעת החפצים המושחרים שוב נקבל התפלגות אחרת. הבעיה חמורה יותר, שכן מטבע הדברים הסטטיסטיקה שעשינו, זו שהראתה לנו ש-85% מהחפצים נמצאים אצל בעליהם, נעשתה אך ורק על חפצים שהבעלות שלהם מוכרות וידועה, כלומר כולה נעשית על חפצים לא מושחרים, אלו שמחוץ לתחום המצומצם של חפצים שבמחלוקת. השאלה היא מה תהיה התוצאה אם נעשה את הסטטיסטיקה רק על ארבעת החפצים המושחרים. ראינו שאין שום סיבה לחשוב שהתוצאה תהיה שוב 0.85, ובעצם יש סיבה טובה לחשוב שלא. חזקות הכשרות של התובע והנתבע שוות, ולכן אפריורי ההנחה שהתובע משקר לא סבירה יותר מההנחה שהנתבע משקר. עקרונית נראה שההסתברות שנקבל כאן היא משהו כמו 1/2.[2]

במינוח של הסתברויות מותנות, 0.85 הוא ההסתברות של חפץ שנבחר אקראית בעולם להיות ביד בעליו, P(A). אבל אנחנו מחפשים את ההסתברות של חפץ שנבחר מתוך קבוצת העצמים שבמחלוקת (המושחרים). כאן זוהי הסתברות מותנה P(A/B), כאשר B הוא העובדה שהחפץ שנוי במחלוקת (הוא אחד מהמושחרים). החפץ שעליו אנחנו דנים נבחר מתוך תת הקבוצה של אלו שבמחלוקת. ראינו שאפריורית ההסתברות הזאת כנראה שווה למשהו כמו 1/2. אין פלא שהיא קטנה יותר מהתוצאה הכללית, שכן לא נכון להניח זהות בין P(A) לבין P(A/B).

המסקנה היא שגם אם אפשר לדבר על חזקה מה שתחת יד האדם הוא שלו, זה ייתכן רק במשמעות משפטית. אין לחזקה הזאת משמעות הסתברותית. ייתכן שמשפטית אנחנו מניחים חזקה שאם חפץ כלשהו נמצא בידי פלוני אז הוא שלו עד שיוכח אחרת, מסיבות כמו "דכאיב ליה כאיבא ליזיל לבי אסיא" או מכוח פסוק, אבל זו חזקה משפטית ולא טענה הסתברותית. הסתברותית ההתפלגות שווה לשני הצדדים.

התעלמות ממידע: מדגם מייצג והכללות מדעיות

החישוב שמניחים אלו שמזהים בין החזקה הזאת לבין מושג המוחזקות, מתעלם ממידע שיש בידינו (B), ועושים חישוב של הסתברות מוחלטת במקום מותנית. אבל לא נכון להסתמך על התוצאה הכללית אם יש  לנו מידע ספציפי יותר. זה בדיוק כמו להציע שהסיכוי לקבל 5 כשידוע שהתוצאה היא אי זוגית, הוא 1/6, שכן זוהי התוצאה לסיכוי המוחלט לקבל 5. במקרה של הטלת הקובייה, התוצאה המותנית גדלה (מ-1/6 ל-1/3) ואילו אצלנו היא קטנה (מ-0.85 ל-0.5), אבל כך או כך זוהי טעות. אסור להתעלם ממידע שבידינו ולעשות סטטיסטיקה על בסיס מידע חלקי. אנחנו מאבדים מידע ולכן התוצאה שבידינו פחות מדויקת.

לכאורה המדע עושה בדיוק את אותה טעות. אנחנו צופים בכמה עצמים בעלי מסה שנופלים לכדור הארץ, ומסיקים מכאן חוק כללי שכל העצמים בעלי המסה ייפלו לכדור הארץ. לכאורה גם כאן יש הסקה מקבוצה חלקית לקבוצה הכללית. אבל שימו לב שהמדע לפחות משתדל שהמדגם שלו יהיה מייצג, כלומר שההתפלגות שבתוך הקבוצה החלקית תהיה דומה לזו שבקבוצה הכללית. משמעות הדבר היא שלא התעלמנו ממידע. אם לוקחים קבוצה חלקית שאין לה מאפיין מיוחד נוסף על פני הקבוצה הכללית, אזי גם אם צמצמנו את הקבוצה לא התעלמנו ממידע. ההתפלגות בקבוצה החלקית תהיה דומה לזו שבקבוצה המלאה. אם היינו בודקים 5% מהחפצים בעולם ומגלים ש-85% מהם מצויים בידי בעליהם, אזי בהחלט סביר לומר שזו כנאה גם ההתפלגות הכללית. זאת כל עוד לקבוצה הקטנה הזאת אין מאפיין מיוחד שונה ממאפייניה של הקבוצה הגדולה. זהו מדגם מייצג, שכן השימוש בו אינו מתעלם ממידע. אבל אם היינו עושים את ההכללה של חוק הגרביטציה על בסיס קבוצת עצמים שכולם עשויים מעץ, אזי ההכללה שכל העצמים בעלי המסה נופלים לכדור הארץ הייתה בעייתית מאד. התעלמנו מהמידע שכל העצמים בקבוצה שבדקנו (המדגם) עשויים עץ. ייתכן שרק עצמים שעשויים מעץ נופלים לכדור הארץ. זהו מדגם לא מייצג, מפני שיש לו מאפיינים ייחודיים (יש בו עוד מידע שאסור להתעלם ממנו).

אם הייתי מסיק מסקנות מההתפלגות הכללית בכלל האליפסה שלמעלה אל הקבוצה שנמצאת משמאל לקו הגבול שמצויר שם, זה היה לגיטימי, כל עוד לא ידוע לי מאפיין מיוחד לחפצים שבתת הקבוצה הזאת. אבל ההנחה שמזהה מוחזקות עם "חזקה מה שתחת יד האדם הוא שלו" עושה קפיצה לא לגיטימית. היא משתמשת בהתפלגות של כלל החפצים באליפסה כדי לתאר את מה שמצוי בקו הגבול הזה. כאן יש תכונה מיוחדת לתת הקבוצה שבה אנחנו דנים, שכן החפצים בתת הקבוצה הזאת כולם מצויים במחלוקת משפטית. היסק כזה מתעלם ממידע רלוונטי ולכן מעלה תוצאה סטטיסטית לא נכונה.

דוגמה נוספת: בעיית מונטי הול

זוהי בעיה הסתברותית ידועה, שמקור שמה בשעשועון טלוויזיה אמריקאי (בהנחיית מונטי הול). במסגרת המשחק מציגים בפני השחקן שלוש דלתות. מאחורי אחת מהן מצוי פרס יקר ערך – מכונית – ומאחורי כל אחת משתי הדלתות האחרות נמצאת עז. השחקן צריך לפתוח דלת ואז הוא זוכה במה שנמצא מאחוריה. הוא מעדיף כמובן את המכונית, אבל הוא אינו יודע איזו דלת מסתירה אותה, ולכן נאלץ לבחור באקראי. אלא שכעת יש טוויסט בעלילה. לאחר שהשחקן הצביע ובחר את אחת הדלתות, נניח דלת מס׳ 1, המנחה, היודע מהי הדלת שמסתירה את המכונית, פותח אחת משתי הדלתות האחרות, נניח דלת מס׳ 3, ומגלה מאחוריה עז (הוא תמיד בוחר דלת שמאחוריה עז). כעת מאפשרים לשחקן להחליט האם לדבוק בבחירה המקורית שלו, או לשנות את ההחלטה ולהעדיף במקומה את הדלת האחרונה שנותרה סגורה – דלת מס׳ 2. האם כדאי לו לשנות כעת את בחירתו או שזה לא משנה?

לכאורה הסיכוי הראשוני שהשחקן בחר כבר בהתחלה בדלת עם המכונית הוא 1/3 (אחת משלוש דלתות). בנוסף, ברור לשחקן שמאחורי לפחות אחת משתי הדלתות הנותרות הייתה עז. המנחה פתח את הדלת שמאחוריה יש עז כי הוא יודע מה יש מאחורי כל דלת, ולכן לכאורה לא הוסיף בכך שום מידע לשחקן. תמיד יש דלת עם עז והוא יכול לבחור בה. אם כן, ההסתברות לכך שהמכונית נמצאת מאחורי כל דלת נותרת 1/3. מאידך, כעת השחקן עומד בפני שתי דלתות וכעת הוא  יודע שמאחורי אחת מהן יש עז ומאחורי השנייה יש מכונית. אם כן, כעת הסיכוי לכל אחת מהן הוא 1/2. אבל שימו לב שזהו הסיכוי גם לדלת שבה הוא בחר מראש, ולכן עדיין לא נראה שיש לו סיבה להחליף את בחירתו. לכאורה המסקנה היא שאין טעם להחליף, כי זה לא ישנה מאומה.

אך זוהי טעות. חישוב  סטטיסטי מראה שתמיד כדאי לו להחליף את בחירתו. הבחירה המקורית הייתה בסיכוי 1/3 לזכייה. המנחה תמיד ישאיר שתי דלתות נעולות שמאחורי אחת  מהן יש מכונית, אבל הוא עושה זאת על ידי פתיחה של דלת שהוא יודע מראש שמאחוריה אין מכונית. לכן בעצם הוא כן מוסיף מידע לשחקן. הדלת שבה השחקן בחר מראש יש לה סיכוי זכייה של 1/3 כפי שהיה מראש. לגביה לא השתנה מאומה שהרי המנחה תמיד ישאיר אותו עם אותו דלת והסיכוי מראש היה 1/3. אבל סיכויי הזכייה של הדלת השנייה עולים מ-1/3 ל-2/3, שכן היא מנקזת אליה את כל הסיכויים שהמכונית לא נמצאת מאחורי הדלת שנבחרה על ידי השחקן. בכך הוא הוסיף לשחקן מידע לגבי הדלת ההיא ולכן כדאי לו לבחור בה. העוקץ הוא שהמנחה לא בוחר סתם דלת ומוצא במקרה מאחוריה עז. הוא בוחר דלת שהוא יודע מראש שיש מאחוריה עז. שימו לב שקיבלנו את התוצאה שהסיכוי למכונית מאחורי הדלת השנייה אינו 1/2 אלא 2/3 (אחרת סכום ההסתברויות 1/2+ 1/3 אינו 1). עסק מבלבל למדיי.

המוקש כאן נעוץ כמובן בהסתברות מותנה. בתחילת המשחק, ההסתברות לדלת הנותרת היא 1/3, כמו שתי הדלתות אחרות. אבל אחרי שהמנחה פותח את הדלת שפתח, הוא נתן לנו מידע נוסף. כעת ההסתברות של הדלת הנותרת (A) בהינתן שהיא נבחרה על ידי המנחה להישאר סגורה עלתה ל-2/3. לכן אל לנו ללכת אחרי ההסתברות המוחלטת P(A), שבהיעדר מידע על הדלתות שווה ל-1/3 (כמו הסיכוי של הדלת הנוכחית). עלינו להשתמש בהסתברות מותנה שמתחשבת במידע שנוסף לנו: P(A/Z) = 2/3, כאשר A הוא האירוע שהמכונית נמצאת מאחורי הדלת הנותרת, ו-Z הוא האירוע שהמנחה השאיר את דלת הזאת סגורה. הסיכוי הזה גדול פי 2 מהסיכוי של הדלת שנבחרה. לכן כדאי להחליף דלתות.

זוהי דוגמה נוספת לבלבול שקורה בין הסתברות מוחלטת להסתברות מותנה. גם כאן ניתן להיווכח שמשמעות הערבוב בין ההסתברויות היא שאנחנו מתעלמים ממידע שקיים בידינו.

עץ אפשרויות, מרחב מאורעות ומידע

כדי לנתח את המקרה הזה במונחים שראינו למעלה, עלינו לתאר את המשחק במונחי עץ אפשרויות (כפי שתיארתי בשני הטורים הקודמים). יש לנו שלוש דלתות: {A,B,C}, כאשר אנחנו קוראים לדלת שהמכונית נמצאת מאחוריה A. מאחורי שתי האחרות יש עזים. הסיכוי של השחקן לבחור בדלת A הוא 1/3. הסיכוי שלו לבחור בכל אחת משתי האחרות גם הוא 1/3, וביחד 2/3.

בהנחה שהשחקן בחר בדלת A, המנחה יפתח דלת עם עז וישאיר דלת אחרת עם עז סגורה. במקרים הללו כדאי לשחקן להישאר עם הדלת שלו. אם השחקן בחר בדלת עם עז (נאמר B) אזי המנחה יפתח את דלת C (בסיכוי 1) וישאיר את A סגורה. אותו דבר אם השחקן בוחר את C. בשני המקרים הללו כדאי לשחקן להחליף דלת.

כעת נעשה את חישוב ההסתברויות. הסיכוי לכל בחירה בהתחלה הוא 1/3. אם השחקן בחר A אז יש סיכוי 1/2 לכל אחד מהענפים שתחתיו.[3] בסה"כ הסיכוי 1/3*1/2*2=1/3 שכדאי להישאר עם הדלת שבחר. אם השחקן בחר B או C אז יש לנו בסה"כ סיכוי 1/3*1+1/3*1=2/3 שכדאי להחליף דלת. לכן בשורה התחתונה עדיף לו להחליף דלת.

המידע שנוסף לשחקן הוא שהבחירה שלו כעת נמצאת בצמתים השניים ולא בצומת הראשונה, כלומר הוא נמצא כעת אחרי הפעולה של המנחה. ניתן לדבר על כך גם במונחי צמצום מרחב המאורעות. אם נספור את מספר האפשרויות שהחלפת דלת תביא לרווח, נגלה שאחרי הפעולה של המנחה יש אחוז יותר גבוה של כאלה מכלל המקרים לעומת אחוזם בשלב שלפני פעולת המנחה.

מסקנה

הסתברות היא מערכת כלים לקבלת החלטות בתנאים של חוסר במידע. לכן תוצאת החישוב תלויה לא רק בסיטואציה העובדתית (הוגנות הקובייה, מסת הגוף וכו') אלא גם במידע החסר ובמידע שישנו בידינו. אם נשנה את כמות המידע שבידינו התוצאה של החישוב לגבי אותו מקרה עצמו יכולה להיות שונה. זה יקרה כאשר המידע שהתעלמנו ממנו או שנוסף לנו הוא רלוונטי, כלומר אם מדובר במידע שהתוצאה תלויה בו סטטיסטית. התלות הסטטיסטית היא שקובעת את הרלוונטיות של המידע שבו יש להתחשב.

במאמרי "על כשל היציגות בהלכה" הבאתי כמה דוגמאות נוספות לכשלים של הסתברות מותנה, ובלשון ההלכתית זה נקרא "רוב שאיתרע".

רוב שאיתרע: ייבום

בסוף המאמר הבאתי שתי דוגמאות של רוב שאיתרע. זה מדבר על מצב שבו יש רוב לטובת אפשרות אחת על פני אחרת, ואז מתגלה לנו מידע נוסף והרוב מתרועע. זהו ממש ביטוי הלכתי למצב של מידע נוסף שמשנה את ההתפלגות.

הדוגמה הראשונה היא במשנה יבמות לה ע"ב:

ספק בן תשעה לראשון, ספק בן שבעה לאחרון – יוציא, והולד כשר, וחייבין באשם תלוי.

מדובר במי שהקדים וייבם את יבמתו מיד אחרי מות אחיו, ולאחר מכן נולד לה בן בעיתוי שמעורר ספק. הגמרא מניחה שעובר יכול להיוולד או אחרי תשעה חודשים או אחרי שבעה חודשים, כשהרוב נולדים אחרי תשעה. כאן הספק הוא האם התינוק נולד אחרי תשעה חודשי היריון ואביו הוא הראשון, או שהוא נולד אחרי שבעה חודשי היריון ואביו הוא השני. לצורך הדוגמא נניח שהוא ייבם אותה חודשיים לאחר מות אחיו.

הבן כמובן כשר בכל מקרה (אם הוא של הראשון, אז אמנם הייבום אינו תקף והם עברו עבירת אשת אח שלא במקום מצווה, אבל הוולד ודאי כשר. ואם הוא בן שבעה לשני אז הייבום תקף והוא בנו הכשר של השני). השאלה היא לגבי שני בני הזוג. הם מביאים אשם תלוי בגלל ספק בעילה של אשת אח שלא במקום מצווה (אם היא הייתה בהיריון אין מצוות ייבום ואז היא ערווה כאשת אח על היבם).

הגמרא שם, לז ע"א, מקשה על כך:

ספק בן תשע וכו'. אמר ליה רבא לרב נחמן, לימא: הלך אחר רוב נשים, ורוב נשים לתשעה ילדן!

הגמרא שואלת מדוע הילד נחשב כספק, הרי יש רוב שיולדות לתשעה, ולכן יש להכריע שהוא בנו של הראשון, ולכן חיוב הקרבן צריך להיות של חטאת ודאית ולא של אשם תלוי.

במסקנה הגמרא מסבירה זאת כך:

…א"ל, הכי קאמינא: רוב נשים ילדן לתשעה, ומיעוט –  לשבעה, וכל היולדת לתשעה – עוברה ניכר לשליש ימיה, וזו הואיל ולא הוכר עוברה לשליש ימיה – איתרע ליה רובא.

בשלב זה הגמרא מציעה שכל היולדות לט' עוברן ניכר. וכאן הרי מדובר בעובר שלא ניכר (לכן היבם החליט לייבם אותה כי חשב שאינה בהיריון. אם העובר היה ניכר בשעת הייבום לא היה מתעורר כאן הספק). ומכיון שהיולדות לט' עוברן ניכר, איתרע הרוב שיולדות לט'.

כעת מקשה הגמרא:

אי כל היולדת לתשעה – עוברה ניכר לשליש ימיה, הא מדלא הוכר לשליש ימיה – עוברה ודאי בר שבעה לבתראה הוא!

אם אכן כל היולדות לט' עוברן ניכר, אזי הדין לא היה צריך להיות שהם חייבים אשם תלוי, אלא שהם פטורים, כי יש וודאות שהוא נולד לז'.

לבסוף הגמרא מתקנת שזו לא וודאות שהעובר ניכר ביולדת לט', אלא זהו רוב:

אלא אימא: רוב היולדת לתשעה – עוברה ניכר לשליש ימיה, והאי מדלא הוכר לשליש ימיה – איתרע ליה רובא.

אם כן, למסקנה הגמרא מסבירה שהרוב שיולדות לתשעה איתרע בגלל שמבין היולדות לט' הרוב עוברן ניכר. לכן הרוב שיולדות לתשעה איתרע, והוי מצב של ספק, ולכן הם חייבים אשם תלוי.

התשובה לא ברורה. אם העובר כאן לא ניכר (וראינו שזהו המצב) הרי יש רוב לכיוון הנגדי, שהעובר הזה לא נולד לט'. אם כן, מדוע לא נחליט כאן שהעובר הזה נולד לז', ונפטור אותם בכלל מקרבן?

רוב שאיתרע: בתולין

ישנו מהלך מקביל לגמרי בסוגיית כתובות טז סוע"א. הגמרא שם עוסקת בשאלה האם האישה שבפנינו נישאה כבתולה או לא. ההנחה היא שלא הגיע אלינו קול על כך שהיא נישאה בתולה. מאידך, יש רוב מהנישאות שהן בתולות. על כך אומרת הגמרא שם:

אמר רבינא, משום דאיכא למימר: רוב נשים בתולות נישאות ומיעוט אלמנות, וכל הנשאת בתולה יש לה קול, וזו הואיל ואין לה קול – איתרע לה רובא.

יש רוב שנישאות בתולות. והרוב איתרע בגלל שכל הנישאות בתולות יש להן קול.

כעת מקשה הגמרא שאם הכלל שהנישאות בתולות יש להם קול הוא וודאות ולא רוב, אז לא רק שהרוב איתרע אלא יש בירור הפוך:

אי כל הנשאת בתולה יש לה קול, כי אתו עדים מאי הוי? הנך סהדי שקרי נינהו!

ולמסקנה הגמרא מסבירה שזהו רוב ולא וודאות:

אלא אמר רבינא: רוב הנשאת בתולה יש לה קול, וזו הואיל ואין לה קול – איתרע לה רובא.

כאמור, המהלך ממש מקביל לסוגיית יבמות. וגם כאן ניתן לשאול אם יש רוב נישאות בתולות שיש להן קול, אזי מי שנישאה בלא קול היא כנראה לא בתולה. אז מדוע זה ספק ולא ודאי לכיוון ההפוך?

הסבר: הסתברות מותנה

התשובה לשני הקשיים הללו פשוטה למדיי, ונראה אותה דרך הדוגמה השנייה. יש רוב מבין הנשים הנישאות שהן בתולות. לכן באופן כללי אם נשאל האם האישה שבפנינו נישאה בעולה או בתולה – התשובה תהיה בתולה. מאידך, אם לא יצא עליה קול אז יש רוב נגדי שכן הרוב מבין הנישאות בתולות יוצא עליהן קול. נניח שיש בעולם 1000 נשים שנישאו. מתוכן 80% בתולות, כלומר יש 800 בתולות, ו-200 בעולות. לעומת זאת, מתוך הבתולות יש רוב של 80% שיוצא עליהן קול, כלומר יש 640 בתולות שיצא עליהן קול, וממילא 160 בתולות שנישאו ולא יצא עליהן קול. כעת באה לפנינו אישה שנישאה ללא קול, ואנחנו מתלבטים האם היא בתולה או בעולה. כדי להכריע אנחנו משווים את מספר הנישאות בעולות (200) למספר הבתולות ללא קול (160). ההכרעה ברורה: היא בעולה. הרוב השני ניטרל את הרוב הראשון. זהו המכניזם של רוב שאיתרע על ידי רוב נגדי.

בשיעורי ר' שמואל רוזובסקי למסכת יבמות, סי' שצט, עמד גם הוא על הקושי הזה, והוא ניסח אותו כך:

והנה בפשטות מיירי דהרוב השני הוא באותו יחס של הרוב הראשון ודרך משל אם הרוב הראשון דרוב נשים ילדן לתשעה הוי ביחס של ד' לה' וכגון דמתוך מאה נשים יולדות שמונים לתשעה א"כ הרוב השני דרוב היולדות לתשעה עוברן ניכר הוי נמי ביחס של ד' לה' דהיינו ס"ד מתוך השמונים דילדן לתשעה ולפי"ז נמצא דמתוך ק' נשים יש כ' נשים דיולדות לז' ועוד ט"ז נשים דאין עוברן ניכר וא"כ צ"ע דהא הך אשה הויא בודאי מחד מהנהו מיעוטי ואינה משאר הנשים היולדות לט' ועוברן ניכר וכיון שכן צ"ע אמאי מספקינן בה מהיכן היא הרי יש רוב שהיא מהיולדות לז' שהרי היולדות לז' הוו טפי מן היולדות לט' ואין עוברן ניכר?

ודוחק לומר דמיירי הכא דוקא בכה"ג שהרוב השני אינו באותו יחס של הרוב הראשון אלא מתוך פ' היולדות לתשעה יש כ' נשים שאין עוברן ניכר ואין היולדות לז' מרובות מהיולדות לט' ואין עוברן ניכר דבפשטות לא משמע דמיירי בכה"ג אלא היחס בין המיעוט לרוב ברוב בתרא הוי כמו היחס בין המיעוט לרוב ברוב קמא וצ"ע.

אם שני הרובים הם באותה עוצמה נוצר כאן רוב מנוגד, כפי שראינו למעלה. אם כן, מקשה הרש"ר, מדוע אנחנו מתייחסים לזה כמצב של ספק (שהרוב איתרע) ולא כמצב וודאי? לכאורה יש כאן הכרעה לכיוון הנגדי ולא מצב של ספק.

ברור שהתשובה לשאלה זו תלויה ביחס בין שני הרובים. אם רוב הבתולות שנישאות עם קול היה פחות משמעותי, לדוגמא 60%, אזי מספר הבתולות שנישאו ללא קול היה רק 320. לעומת מספר הנישאות בעולות שהוא 200. אם כן, כעת כשתבוא לפנינו אישה שנישאה ללא קול ההכרעה תהיה עדיין שהיא בתולה. כאן הרוב לא איתרע. ברוב של 75% מהבתולות שנישאות עם קול, שני הגדלים ישתוו, ואנחנו נישאר במצב של ספק. אם כן, לעצם קושייתו של הרש"ר, יש ליישב שההלכה קובעת קטגורית שכאשר רוב איתרע אנחנו לא מתחשבים בו. אין לנו אפשרות לעשות סקר סטטיסטי בכל מקרה שמגיע לפני בי"ד כדי לדעת את יחס הרובים, ולכן ההנחה היא שהמצב שקול ואין דרך להכריע משיקולי רוב. מבחינה הלכתית זהו מצב של ספק.

ברקע הדברים חשוב לחזור על מה שראינו בשני הטורים הקודמים. כמעט בכל המקרים של רוב בהלכה מדובר ברוב נגטיבי, כלומר רוב שאיננו יודעים לקבוע את שיעורו. במצב כזה הדרך הנכונה ביותר היא לקבוע קביעה כללית שכשרוב כלשהו איתרע הוא מתבטל ואין לסמוך עליו. אם מדובר ברוב פוזיטיבי, אזי באמת אין צורך להיזקק לרוב שאיתרע ואפשר לעשות את החישוב וללכת אחרי הרוב כפי שהוא. אבל ברוב נגטיבי אין אפשרות להסתמך על רוב במצב כזה ולכן באמת יש לדחות רוב שאיתרע. אגב, המושג רוב שאיתרע הוא הביטוי ההלכתי להערתי בתחילת טור 612, שם עמדתי על כך שלפעמים יש רובא דרובא כשהרוב השני הולך נגד הראשון ולא איתו. במצב כזה יכול להיווצר קיזוז ונאבד את הרוב הראשוני. זהו בדיוק המקרה של רוב דאיתרע. רוב דאיתרע הוא תמונת הראי של 'רובא דרובא', עם אותו עץ אפשרויות, אלא שב'רובא דרובא' הרוב השני מחזק את הראשון וב'רוב דאיתרע' הוא מחליש אותו.

כעת אנחנו מגיעים לכשל של ההסתברות המותנה. הרוב הראשוני הוא הסתברות מוחלטת שנכונה לכלל האוכלוסייה (רוב הנשים נישאות בתולות). אבל לגבי האישה שבפנינו יש לנו עוד מידע רלוונטי: לא היה עליה קול של בתולין. המידע הזה מצמצם את הקבוצה של כלל הנשים לנשים מסוימות (אלו שאין עליהן קול של בתולין). המידע הזה שמצמצם את הקבוצה הרלוונטית הופך את ההסתברות המוחלטת להסתברות מותנה, ולכן הסיכוי משתנה. בתת הקבוצה המיוחדת הזאת, ההתפלגות היא שונה, וזה בדיוק מה שהתלמוד מכנה רוב שהתרועע.

הקשר לטורים הקודמים

ניתן להציג 'רוב דאיתרע' בצורה של עץ אפשרויות, כמו שעשינו בשני הטורים הקודמים וכאן למעלה. בצומת העליונה שני הענפים מתייחסים לזה לזה דרך הרוב הראשון (האם היא שייכת לנישאות בתולות או לא), ובצמתים שלמטה שולט הרוב השני (אם היא שייכת לרוב הבתולות, יש לדון האם יצא עליה קול או לא),[4] אבל כאמור הכיוון של שני הרובים כאן הוא הפוך.

מצב  כזה כמובן גם ניתן לייצוג באמצעות שרטוט של אליפסה כמו שעשינו כאן. ניקח את כלל הנשים הנשואות שמיוצג על ידי האליפסה. מתוכן הרוב נישאות בתולות והמיעוט לא. בתוך הקבוצה של אלו שנישאו בתולות יש רוב שיצא עליהן קול שהן בתולות ומיעוט שנישאו בתולות בלי שיצא עליהן קול. התמונה היא הבאה:

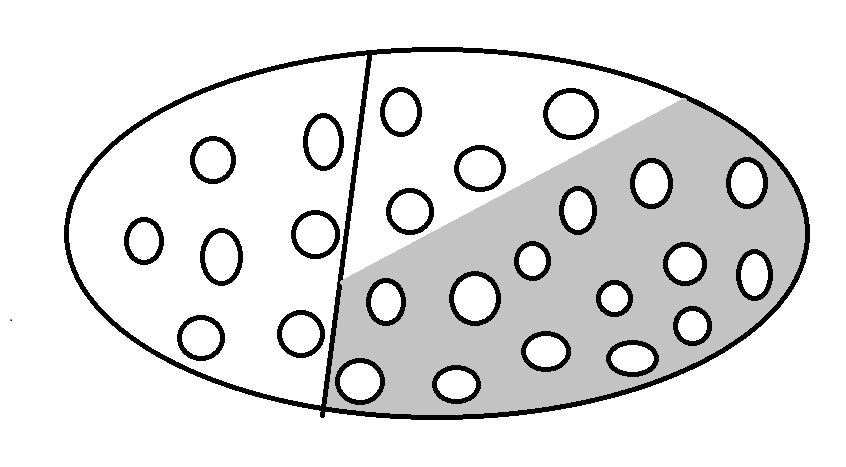
הצד השמאלי של האליפסה הוא המיעוט שלא נישאות בתולות. בצד הימני זהו הרוב שנישאות בתולות. הרוב של תת הקבוצה הימנית (שמסומן באזור הכהה) יוצא קול על היותן בתולות, והמיעוט של אותה קבוצה נישאות בתולות בלי קול (זהו החלק הלבן שמעל האזור הכהה בצד ימין של האליפסה).

כעת מגיעה לפנינו אישה שלא יצא עליה קול כשנישאה. בהנחה שהאישה שייכת לאלו שנישאו בלי קול, היא שייכת לתת קבוצה של האליפסה שיש לנו מידע רלוונטי לגביה (שלא יצא עליהן קול). תת הקבוצה הזאת היא כלל האזור הלבן באליפסה. ועדיין אנחנו מתלבטים לאיזו תת קבוצה של האזור הלבן היא שייכת: האם היא שייכת לאלו שנישאו בעולות (הצד השמאלי) ולכן לא יצא עליהן קול, או שהיא נישאה בתולה אבל בלי קול (הצד הימני העליון). זוהי התפלגות פנימית של קבוצת אלו שלא יצא עליהן קול, וכפי שתוכלו לראות בתוך תת הקבוצה הזאת (האזור הלבן) אין בהכרח רוב לאלו שנישאו בתולות. זה תלוי בגודלן של שתי תת הקבוצות הללו. בדוגמה שלמעלה, יש יחס 7:4 לטובת זה שהיא לא נישאה בתולה. שימו לב שזה קורה למרות שבכלל הנשים בעולם הרוב נישאות בתולות. זוהי המחשה של צמצום המרחב על פי מידע רלוונטי, שבמרחב המצומצם ההתפלגות היא שונה מאשר בכלל המרחב. יש כאן שוב תופעה של הסתברות מותנה, ואסור לערבב אותה עם הסתברות מלאה. למרות שבמכלול רוב הנשים נישאות בתולות, כשידוע שלא יצא קול ההתפלגות שונה, וייתכן שאין רוב לבתולות. במצב כזה אנחנו אומרים שהרוב הראשון איתרע ולא משתמשים בו, וזאת כמובן כאשר הרוב שבו מדובר הוא נגטיבי (אין לנו מידע מספרי עליו). ברוב פוזיטיבי כשיש לנו מידע מספרי, אנחנו פשוט בודקים האם בשורה התחתונה נותר רוב או לא.

'דבר מה' בהפללה עצמית ודיאגנוזה רפואית

במאמרי הנ"ל הסברתי שכשלי יציגות בעצם עוסקים בהשוואה בין המכלול לבין מדגם לא מייצג, וכפי שראינו כאן פירוש הדבר הוא שההתפלגות במדגם שונה מההתפלגות בכלל האוכלוסייה, ולכן יש להשתמש בהתפלגות מותנה (בהינתן שאתה שייך לתת הקבוצה הזאת, כלומר למדגם, מה הסיכוי לכך וכך?). ראינו שם השלכות לגבי דיאגנוזה רפואית של מחלות נדירות ולגבי ראיות משפטיות (הדרישה לתוספת של 'דבר מה' ראייתי בנוסף להפללה העצמית). כאן רק אדגים את הדברים בקצרה כדי להראות את הקשר אלינו (לפירוט נוסף ראו במאמרי הנ"ל).

ישנן מערכות חוק שבהן הודאה נחשבת כמלכת הראיות, ולכן אדם שמפליל את עצמו מורשע שם בדין. אבל בחוק הישראלי לא די בהפללה עצמית (אלא אם ניתנה בבית המשפט עצמו), אם כי רואים הודאה כזאת כראיה חזקה מאד. כדי להרשיע אם שהפליל את עצמו נדרש עוד 'דבר מה', כלומר עוד ראיה נוספת אפילו אם היא כשלעצמה חלשה למדיי. כך אנו מוצאים בהנחיות היועץ המשפטי לממשלה, הנחיה מס' 4.3012, מתאריך ניסן תשס"ז (אפריל 2007) סעיף 1:[5]

כלל נקוט בפסיקתו של בית המשפט העליון, מימים ימימה, כי אין להרשיע אדם על סמך הודאתו בלבד אשר נמסרה מחוץ לכותלי בית המשפט, גם כאשר הודאה זו נתקבלה ללא לחץ חיצוני, אלא אם כן נמצא "דבר מה נוסף" לחיזוק אותה הודאה (ע"פ 3/49 אנדלרסקי נ' היועץ המשפטי לממשלה, פ"ד ב 589; ע"פ 290/59, פלוני נ' היועץ המשפטי לממשלה, פ"ד יד 1489).

מדוע חשובה כל כך תוספת של דבר מה? מדובר על ראיה חלשה למדיי מצד עצמה, אבל כפי שנראה כעת כאשר היא נוספת להפללה עצמית היא משנה לגמרי את התמונה.

במאמרי הצעתי להסביר גם את זה במונחי הסתברות מותנה וכשל היציגות. נניח לצורך הדיון שמדובר בעבירת רצח. נניח עוד שהפללה עצמית היא ראיה בעוצמה של 99%. אבל רצח הוא עניין נדיר מאד, כלומר מספר הרוצחים באוכלוסייה הכללית הוא הרבה פחות מ-1%. נניח לצורך הדיון שמדובר על 0.01%. הראיתי שם שבמצב כזה חוזק הראיה המעשי הוא בערך 1% אמינות. שימו לב, למרות שמדובר במלכת הראיות, עדיין כשהיא מוכיחה תופעה נדירה היא לא בהכרח אמינה. מה שקובע הוא היחס בין הנדירות של התופעה לבין איכות הראיה, ובמקרה זה שכיחות התופעה קטנה פי מאה מאיכות הראיה, ולכן הראיה אינה טובה (ראו שם את החישוב וההסבר). כפי שהראיתי שם, אותו מצב בדיוק קיים ביחס לדיאגנוזה למחלה נדירה ששכיחותה באוכלוסייה הכללית היא 0.01%, באמצעות בדיקה שאמינותה היא 99%.

נניח כעת שאנחנו מוסיפים דבר מה, למשל ראיה שהנאשם היה באזור הרצח. זה כשלעצמו רחוק מלהספיק כדי להרשיע. האם מישהו היה מרשיע אדם רק בגלל שראו אותו באזור הרצח? יש לא מעט אנשים שהיו באזור הרצח, נניח עשרה. לכן זהו 'דבר מה', שכשלעצמו אין לו משקל ראייתי משמעותי. אבל שימו לב מה קורה כאשר יש הפללה עצמית. הראיה החלשה הזאת מפחיתה את מספר הרוצחים הפוטנציאליים מעשרה מיליון (כלל אזרחי המדינה) לעשרה (אלו שהיו באזור). ביחס לקבוצה הזאת, הסיכוי האפריורי שהנאשם הוא הרוצח הוא 10%, ולכן זה כשלעצמו רחוק מלהספיק להרשעה. אבל בתת הקבוצה הזאת הסיכוי שאדם הוא רוצח כבר לא כה קטן, ובמצב כזה ראיה שעוצמתה 99%, כמו הודאה, הופכת להיות מכריעה. כעת הסיכוי לטעות הוא אפסי וניתן להרשיע אותו. מה עושה ה'דבר מה'? הוא בעצם מוסיף לנו מידע רלוונטי, ובכך מצמצם את מרחב המאורעות לתת קבוצה של המרחב הכללי (במקום עשרה מיליון בני אדם חשודים יש עשרה). בתת הקבוצה הזאת ההתפלגות שאותו אדם רוצח היא שונה לגמרי (הסיכוי הוא 10% במקום 0.01%). בלי ה'דבר מה' הראיה מנסה לתת תשובה לשאלה מוחלטת: מה הסיכוי שאדם זה רצח? אבל אחרי ה'דבר מה', הראיה שלנו מעריכה הסתברות מותנה: מה הסיכוי שהוא הרוצח בהינתן שהוא היה באזור הרצח? כאן הראיה (ההפללה העצמית) נותנת לנו סיכוי מצוין.

כך גם לגבי דיאגנוזה רפואית של מחלה נדירה. אם יש לי סימפטום כלשהו בנוסף לבדיקה האמינה שהזכרתי, הסימפטום הזה רחוק מלהספיק לדיאגנוזה מצד עצמו. אבל הוא משנה את הקבוצה שבה מדובר מכלל האנשים לתת קבוצה קטנה של אלו שמופיע אצלם הסימפטום הזה. בתת הקבוצה הזאת השכיחות של המחלה כבר משמעותית יותר, ולכן הבדיקה תיתן תוצאות טובות מאד (כי כאן היא מודדת הסתברות מותנה ולא הסתברות מוחלטת).

בשני המקרים המכניזם זהה: מדובר במעבר מהסתברות מוחלטת, שהיא קטנה  מאד, להסתברות מותנה (הסתברות בתוך קבוצה מצומצמת שיש לנו מידע נוסף B לגביה), שגדולה הרבה יותר. במקרה המשפטי אנחנו שואלים מה הסיכוי שפלוני שהודה הוא רוצח (A) בהינתן שהוא היה באזור (B), שנסמן כהסתברות מותנה: P(A/B). זה כמובן שונה מאד מהשאלה מה הסיכוי שפלוני שהודה הוא הרוצח, P(A). ההסתברות הראשונה גדולה בהרבה, ודי בה כדי להרשיע מעבר לספק סביר. הוא הדין לגבי השאלה מה הסיכוי שפלוני שנמצא חיובי בבדיקה אכן חולה, P(A), לעומת מה הסיכוי שפלוני שנמצא חיובי חולה, בהינתן שיש לו סימפטום רלוונטי, P(A/B). ההסתברות השנייה גדולה בהרבה, ודי בה כדי לתת לנו דיאגנוזה אמינה.

כפי שכתבתי שם, להערכתי מעט מאד משפטנים ורופאים מודעים, מבינים ויודעים להסביר את העניין, ואני חושב שבאמת לא מעטים מהם טעו וטועים בזה לא פעם (רופאים שנותנים דיאגנוזה שגויה או שופטים שמרשיעים על בסיס רעוע). חשבו על רופא ששלח אתכם סתם להיבדק ביחס למחלה נדירה (קורונה) בבדיקה שאמינותה 99%, ויצאה תוצאה חיובית. כעת, שאלו אותו: מה הסיכוי שאני חולה? כמעט אף רופא לא יבין שמדובר בסיכוי קלוש מאד.[6] אני מניח שרובם גם לא יבינו מדוע סימפטום קטן שמעורר חשד רחוק יכול לשנות לגמרי את התמונה הזאת. למזלנו, זהו בדרך כלל המצב. לא שולחים אנשים סתם לבדיקה של מחלות נדירות, אלא אם יש סימפטום שמעורר חשד. הסימפטום הזה הוא ה'דבר מה' ולכן במקרים אלו הבדיקה אכן אמינה. זוהי הסיבה שבדרך כלל בפועל הרופאים לא עושים טעויות כאלה. אבל בבדיקות שגרתיות שלא נעשות עקב חשד ספציפי אצל הפציינט הנבדק (למשל סקר כללי באוכלוסייה), התוצאות עבור אדם מסוים לא שוות מאומה. מעטים מאד מבינים זאת. אבל למזלנו השכל הקולקטיבי בכל זאת עובד איכשהו.

[1] התלבטתי אם נכון יותר לומר 'הסתברות מותנה' או 'הסתברות מותנית'.

[2] המסקנה היא אפילו אבסורדית יותר. אם נסיר מהמרחב את ארבעת המאורעות המושחרים, זוהי הקבוצה שעליה עשינו את הסטטיסטיקה (יש בה 14 חפצים). כאמור, קיבלנו שהסיכוי הוא 0.85 (כלומר בערך 12 מתוך 14 החפצים הם בידי בעליהם). אז הסיכוי לכלל החפצים בעולם (כולל אלו המושחרים) הוא 14/18=0.777. ההסתברות הכללית עצמה לא באמת נכונה כי היא נעשתה רק על החפצים הלבנים. בעצם הטעות אפילו גדולה יותר מאשר ההשערה שהיינו עושים (אם יכולנו) על בסיס כלל החפצים בעולם. כמובן שכמות החפצים שבמחלוקת היא זניחה מול כלל החפצים  בעולם, ולכן במקרה האמתי ההבדל הזה זניח לגמרי.

[3] אני מניח שהמנחה עושה הגרלה בין השתיים. זה לא באמת משנה. יכולתי להתייחס לזה כסיכוי 1 לבחור בדלת עם עז ולהשאיר דלת עם עז סגורה. העדפתי להציג זאת כך כדי להראות את התלות.

[4] תרגיל מעניין לבדוק האם זה מתהפך (ראו בטור הקודם).

[5] ראה על כך בספרי אלוהים משחק בקוביות, ידיעות-ספרים, תל-אביב 2011, עמ' 104-112. שם הסברתי זאת באופן מעט שונה: קריטריון התוחלת אינו אפקטיבי לקבלת החלטות אם הסיכוי לקבל את התוחלת הוא נמוך. ניתן לראות בזה בצורה אחרת גם סוג של כשל יציגות, ואכ"מ.

[6] רובם יאמרו שהסיכוי הוא 99% (שזו כמובן טעות גמורה. אמינות הבדיקה היא הסתברות מותנה הפוכה: אם אני חולה מה הסיכוי שהבדיקה תגלה זאת. הדיאגנוזה עוסקת בהסתברות מותנה הפוכה: אם הבדיקה יצאה חיובית מה הסיכוי שאני חולה. אלו שני מספרים שונים בתכלית, בפרט כשהמחלה שבה מדובר נדירה.